Manacher

对于 Manacher 部分的理解，推荐阅读前有一定了解

##对算法本身的部分理解：

if(2 * maxn - i >= 1)	
    f[i] = min(f[2 * maxn - i],maxr - i);
else	
    f[i] = maxr - i;

关于这个算法，最难以理解的部分也就这里，也就是判断 $i$ 的最长回文长度的下界。

首先定义 $j$ 为 $i$ 关于 $maxn$ 的对称点，$mxr$ 为已有回文半径覆盖到的最右点，$maxn$ 为其的中心点

首先关于 $j$ 的寻找，因为 $maxn = \frac{i-j}{2}$，所以可以化简得：$2\times maxn = i - j$，所以 $j = 2\times maxn - i$

关于第一行的判断条件，也就是在判断 $j$ 的存在，然后看后面的两种情况。

1：若 $f[j] < maxr - i$，我们选择的下界会是 $f[j]$，则有下图

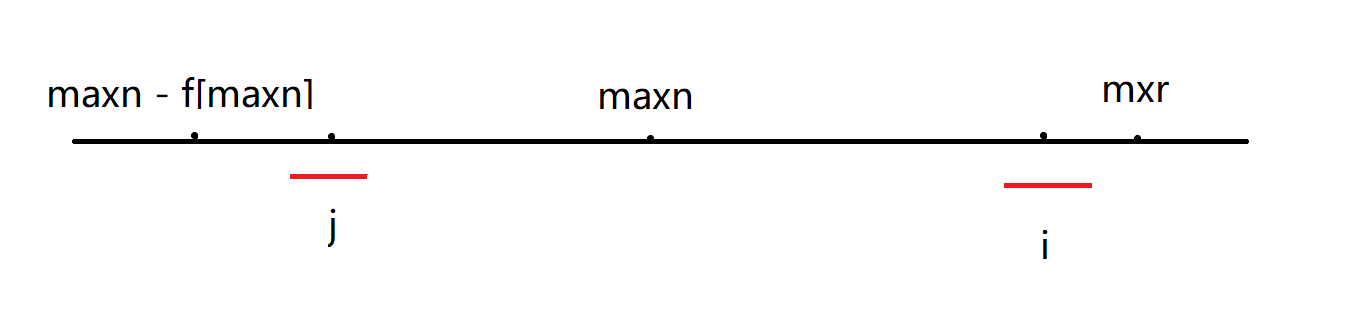
​ 其中用红线代表 $i,j$ 的回文范围，$maxr- i$ 也就是 $i$ 到 $maxr$ 的距离。首先因为这一长段都是以 $maxn$ 为中心的回文子串，所以其实以 $j$ 为中心的回文子串也在以 $i$ 为中心的回文子串那里（不一定完整），因为 $j$ 的回文半径小于 $i$ 到 $maxr$ 的距离，所以以 $j$ 为中心的整个回文串都完整地到了 $i$ 的地方，所以对于 $i$ 来说它的回文半径的下界也就是 $j$ 的回文半径。之所以说是下界，因为超过这个下界的 $i$ 的右边可能有一些值仍然可以和 $i$ 的左边匹配，因为超过部分不一定和 $j$ 那里一样，所以是下界。

2：若 $f[j] > maxr - i$，我们选择的下界会是 $maxr - i$，则有下图：

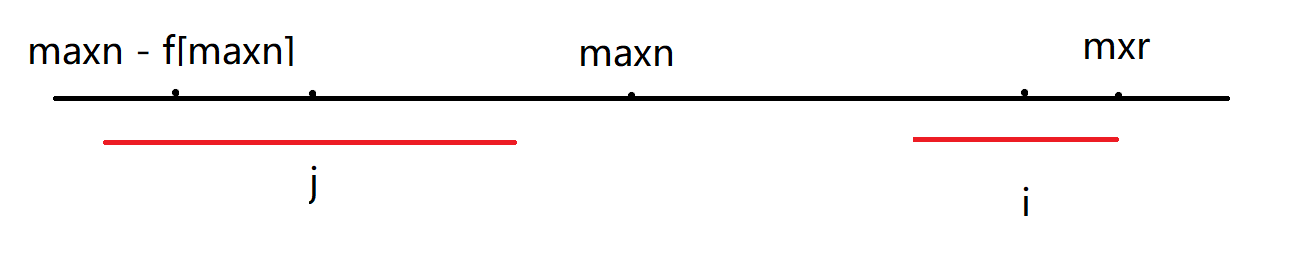
此时也就相当于 $j$ 的回文半径的长度超过了 $maxn$ 的限制，也就是以 $j$ 为中心的回文串只有一部分因为 $maxn$ 的限制而来到了 $i$ 的位置，而这一部分的长度也就是 $j$ 到 $maxn$ 限制的左端点的距离，也就是 $maxr - i$ 那么因为这一段有 $maxn$ 的限制再加上在 $j$ 是回文的，所以也一定是回文的