轻重链剖分

树链剖分的部分理解，推荐阅读前有一定了解

对算法本身的部分理解

if (son[now])
    dfs2(son[now], topf)
for (int i = head[now] i; i = e[i].nxt) {
    int to = e[i].to;
    if (to != fa[now] && to != son[now]) {
        dfs2(to, to);
    }
}

这是第二遍 $dfs$，定义：$son[now]$ 为 $now$ 点的重儿子，$topf$ 为当前的重链上深度最小的一个点也就是开始的点。我们在遍历整棵树的时候，会选择先去遍历这个点的左儿子然后再去管其他的点。我们在这一遍遍历其实就是在给他们分配线段树上的基本信息以及记录轻重链的基本信息，在我们的轻重链剖分的时候，是会将重链看作是线段树上维护的的一段连续区间，先访问重儿子可以使得其的重儿子在线段树上的维护的下标为它加一，也就是说是连续的，也就是一条重链对应连续的一段。

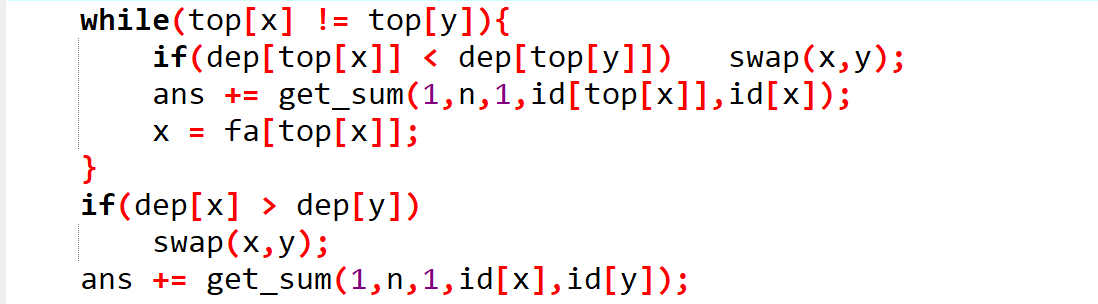
这是寻找 $x,y$ 树上路径的相关信息，定义：$top[x]$ 为 $x$ 节点所在的重链的深度最小的节点（这里节点均为树上的编号），也就是这条重链的开始，$dep[x]$ 为 $x$ 节点在树上的深度，$id[x]$ 为节点 $x$ 在线段树上的编号。也就是这几行代码是在查询树上 $x,y$ 节点之间的路径上经过的节点的权值和。我们一点点地去看。

首先看循环内部，第一个判断条件就是寻找一个重链的起点深度最大的一个，也就是树上最靠下的一个，然后查询这条重链的信息后就直接跳出这条重链，我们考虑跳深度大的一条链一定不会跳过头，而跳深度小的一条链可能会跳过头了，如下图所示：

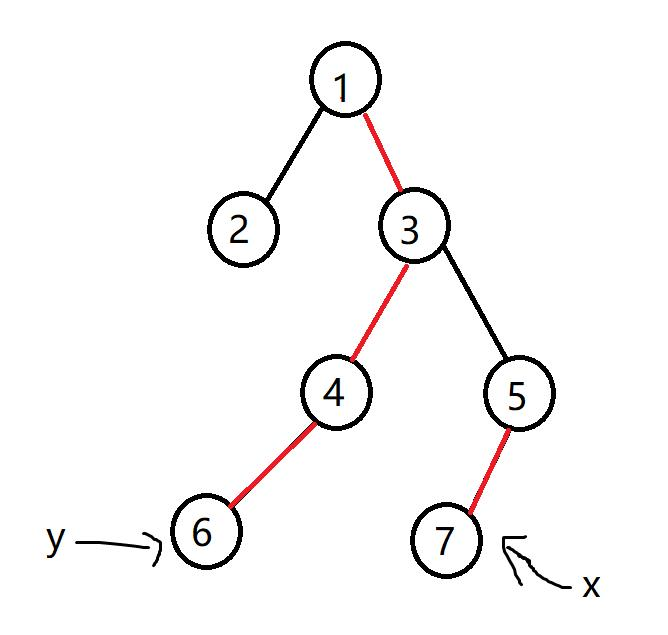
我们以红色边代表重边，以黑色边代表轻边，我们看在这样的情况下如果直接去跳过 $y$ 所在的这条重链，那么就会跳到节点 $1$ 很明显这不正确，所以就会选择跳 $x$ 所在的这条重链，这样不可能会跳出去我们的正确路径。

再看下边的线段树的询问，因为我们的分配线段树上的基本信息是自根到底，所以深度小的节点在线段树上的编号就小，深度大的节点在线段树上的深度就大，所以查询的区间左端点是这条重链的开始，右端点是它本身。

再看下边关于跳过这条重链的情况，我们的 $x$ 跳要跳到其重链的开始的父亲节点，因为如果我们不是跳到父亲结点的话，我们一是会将其重链开始的节点的信息重复计算，二是我们可能下一次跳还是选择这一条重链，但是它的起点就是当前的 $x$ 节点，所以就死循环了。

翻过来看一眼循环条件，这个循环条件相当于是在约束 $x,y$ 不在同一条重链上，因为我们循环是在跳重链，所以如果它们在同一条重链上那么这条重链肯定不能直接跳过了，就应该直接在这条重链上去询问 $x,y$ 的线段树上的相关信息，因为他们在同一重链，所以编号一定是连续的，直接询问那一段就可以了。

最后三行，因为深度大的节点线段树上的编号也大，所以线段树上的区间就是从深度小的节点到深度大的节点。

注意：

我们所给他们分配的线段树上维护的下标或者叫编号就相当于 $dfs$ 序，所以满足 $dfs$ 具有的性质。