大概就是一个数学知识的梳理,可能会有一些地方写的并不是很全很好,未来可能会补。
gcd ( a , b ) = gcd ( b , a % b ) \gcd(a,b) = \gcd(b,a\% b)
g cd( a , b ) = g cd( b , a % b )
求解:
a x + b y = gcd ( a , b ) ax + by = \gcd(a,b)
a x + b y = g cd( a , b )
分析:a x 1 + b y 1 = gcd ( a , b ) ax_1 + by_1 = \gcd(a,b) a x 1 + b y 1 = g cd( a , b ) b x 2 + ( a % b ) y 2 = gcd ( b , a % b ) bx_2 + (a\%b)y_2 = \gcd(b,a\%b) b x 2 + ( a % b ) y 2 = g cd( b , a % b ) gcd ( a , b ) = gcd ( b , a % b ) \gcd(a,b) = \gcd(b,a\%b) g cd( a , b ) = g cd( b , a % b )
a x 1 + b y 1 = b x 2 + ( a % b ) y 2 ax_1 + by_1 = bx_2 + (a\%b)y_2
a x 1 + b y 1 = b x 2 + ( a % b ) y 2
根据 a % b = a − ⌊ a b ⌋ × b a \% b = a - \lfloor \frac{a}{b} \rfloor \times b a % b = a − ⌊ b a ⌋ × b
a x 1 + b y 1 = b x 2 + ( a − ⌊ a b ⌋ × b ) y 2 ax_1 + by_1 = bx_2 + (a - \lfloor \frac{a}{b} \rfloor \times b)y_2
a x 1 + b y 1 = b x 2 + ( a − ⌊ b a ⌋ × b ) y 2
化简一下就有:
a x 1 + b y 1 = a y 2 + b ( x 2 − ⌊ a b ⌋ × b × y 2 ) ax_1 + by_1 = ay_2 + b(x_2 - \lfloor \frac{a}{b} \rfloor \times b \times y_2)
a x 1 + b y 1 = a y 2 + b ( x 2 − ⌊ b a ⌋ × b × y 2 )
必然存在一组解为 x 1 = y 2 , y 1 = x 2 − ⌊ a b ⌋ × b × y 2 x_1 = y_2,y_1 = x_2 - \lfloor \frac{a}{b} \rfloor \times b \times y_2 x 1 = y 2 , y 1 = x 2 − ⌊ b a ⌋ × b × y 2
不断递归下去,当 b = 0 b = 0 b = 0 x = 1 , y = 0 x=1,y=0 x = 1 , y = 0
对于素数 p p p gcd ( a , p ) = 1 \gcd(a,p) = 1 g cd( a , p ) = 1
a p − 1 ≡ 1 m o d p a^{p-1} \equiv 1 \mod p
a p − 1 ≡ 1 m o d p
若 gcd ( a , p ) = 1 \gcd(a,p) = 1 g cd( a , p ) = 1
a φ ( p ) ≡ 1 m o d p a^{\varphi(p)} \equiv 1 \mod p
a φ ( p ) ≡ 1 m o d p
a b = { a b m o d φ ( p ) gcd ( b , p ) = 1 a b gcd ( b , p ) ≠ 1 , b < φ ( p ) a [ b % φ ( p ) + φ ( p ) ] % φ ( p ) gcd ( b , p ) ≠ 1 , b ≥ φ ( p ) a^b =
\begin{cases}
a^{b \mod \varphi(p)} & \gcd(b,p) = 1\\
a^b & \gcd(b,p) \not= 1,b < \varphi(p) \\
a^{[b \% \varphi(p) + \varphi(p)]\% \varphi(p)} & \gcd(b,p) \not= 1,b \ge \varphi(p)
\end{cases}
a b = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ a b m o d φ ( p ) a b a [ b % φ ( p ) + φ ( p ) ] % φ ( p ) g cd( b , p ) = 1 g cd( b , p ) = 1 , b < φ ( p ) g cd( b , p ) = 1 , b ≥ φ ( p )
问题描述:
{ x ≡ a 1 m o d m 1 x ≡ a 2 m o d m 2 ⋯ x ≡ a n m o d m n \begin{cases}
x \equiv a_1 \mod m_1 \\
x \equiv a_2 \mod m_2 \\
\cdots \\
x \equiv a_n \mod m_n
\end{cases}
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ x ≡ a 1 m o d m 1 x ≡ a 2 m o d m 2 ⋯ x ≡ a n m o d m n
其实满足 m 1 , m 2 , ⋯ , m n m_1,m_2,\cdots,m_n m 1 , m 2 , ⋯ , m n
问题分析:M = ∏ i = 1 n a i M = \prod_{i=1}^n a_i M = ∏ i = 1 n a i i i i p i = M m i p_i = \frac{M}{m_i} p i = m i M p i p_i p i m i m_i m i p i − 1 p_i^{-1} p i − 1 c i = p i p i − 1 c_i = p_ip_i^{-1} c i = p i p i − 1 m i m_i m i x = ∑ i = 1 n c i a i m o d M x = \sum_{i=1}^n c_ia_i \mod M x = ∑ i = 1 n c i a i m o d M
考虑合并两个方程:
x ≡ a 1 m o d m 1 x ≡ a 2 m o d m 2 x \equiv a_1 \mod m_1 \\
x \equiv a_2 \mod m_2
x ≡ a 1 m o d m 1 x ≡ a 2 m o d m 2
可以将它们转化为不定方程即:
x = m 1 p + a 1 = m 2 q + a 2 x = m_1p + a_1 = m_2q + a_2
x = m 1 p + a 1 = m 2 q + a 2
转化一下即 m 1 p − m 2 q = a 2 − a 1 m_1p - m_2q = a_2 - a_1 m 1 p − m 2 q = a 2 − a 1 a 2 − a 1 a_2 - a_1 a 2 − a 1 m 1 − m 2 m_1 - m_2 m 1 − m 2 p , q p,q p , q
这样的话就可以将原方程组合并为:x ≡ b m o d M x \equiv b \mod M x ≡ b m o d M b = m 1 p + a 1 , M = lcm ( m 1 , m 2 ) b = m_1p + a_1,M = \text{lcm}(m_1,m_2) b = m 1 p + a 1 , M = lcm ( m 1 , m 2 )
p p p ( p − 1 ) ! ≡ − 1 m o d p (p-1)! \equiv -1 \mod p ( p − 1 ) ! ≡ − 1 m o d p
形式一:p p p ( n m ) \binom{n}{m} ( m n ) p p p n − m n - m n − m p p p ( n + m m ) \binom{n+m}{m} ( m n + m ) p p p n + m n+m n + m
若有两个正整数 n , m n,m n , m p p p
( n m ) = ( n m o d p m m o d p ) × ( ⌊ n p ⌋ ⌊ m p ⌋ ) \binom{n}{m} = \binom{n \mod p}{m \mod p} \times \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor}
( m n ) = ( m m o d p n m o d p ) × ( ⌊ p m ⌋ ⌊ p n ⌋ )
感性的理解就是拆到 p p p
定义: 对于 a ∈ Z , m ∈ N ∗ a \in \mathbb{Z},m \in \mathbb{N}^* a ∈ Z , m ∈ N ∗ ( a , m ) = 1 (a,m) = 1 ( a , m ) = 1 a n ≡ 1 ( m o d m ) a^n \equiv 1 \pmod m a n ≡ 1 ( m o d m ) n n n a a a m m m δ m ( a ) \delta_m(a) δ m ( a ) ord m ( a ) \text{ord}_m(a) ord m ( a )
性质一: a 1 , a 2 , ⋯ , a δ m ( a ) a^1,a^2,\cdots,a^{\delta_m(a)} a 1 , a 2 , ⋯ , a δ m ( a ) m m m
证明:考虑使用反证法,若存在 i ≠ j i \not= j i = j a i ≡ a j ( m o d m ) a^i \equiv a^j \pmod m a i ≡ a j ( m o d m ) a ∣ i − j ∣ ≡ 1 ( m o d m ) a^{|i-j|} \equiv 1 \pmod m a ∣ i − j ∣ ≡ 1 ( m o d m ) 0 < ∣ i − j ∣ < δ m ( a ) 0 < |i-j| < \delta_m(a) 0 < ∣ i − j ∣ < δ m ( a )
性质二: 若 a n ≡ 1 ( m o d m ) a^n \equiv 1 \pmod m a n ≡ 1 ( m o d m ) δ m ( a ) ∣ n \delta_m(a) | n δ m ( a ) ∣ n a p ≡ a q a^p \equiv a^q a p ≡ a q p ≡ q ( m o d δ m ( a ) ) p \equiv q \pmod{\delta_m(a)} p ≡ q ( m o d δ m ( a ) )
性质三: δ m ( a b ) = δ m ( a ) δ m ( b ) \delta_m(ab) = \delta_m(a) \delta_m(b) δ m ( a b ) = δ m ( a ) δ m ( b ) ( δ m ( a ) , δ m ( b ) ) = 1 (\delta_m(a),\delta_m(b)) = 1 ( δ m ( a ) , δ m ( b ) ) = 1
性质四: δ m ( a k ) = δ m ( a ) ( δ m ( a ) , k ) \delta_m(a^k) = \dfrac{\delta_m(a)}{(\delta_m(a),k)} δ m ( a k ) = ( δ m ( a ) , k ) δ m ( a )
所以根据上面这些性质,阶就给了人一种“循环节”的感觉。
若 δ m ( g ) = φ ( m ) \delta_m(g) = \varphi(m) δ m ( g ) = φ ( m ) g g g m m m
性质一: g g g m m m φ ( m ) \varphi(m) φ ( m ) p p p g φ ( m ) p ≢ 1 ( m o d m ) g^{\frac{\varphi(m)}{p}} \not\equiv 1 \pmod m g p φ ( m ) ≡ 1 ( m o d m )
性质二: 若模 m m m φ ( φ ( m ) ) \varphi(\varphi(m)) φ ( φ ( m ) )
性质三: 数 m m m m = 2 , 4 , p α , 2 p α m = 2,4,p^{\alpha},2p^{\alpha} m = 2 , 4 , p α , 2 p α p p p α ∈ N ∗ \alpha \in \mathbb{N}^* α ∈ N ∗
性质四: 最小原根的值为 O ( n 0.25 ) O(n^{0.25}) O ( n 0 . 2 5 )
满足 ( a , p ) = 1 (a,p) = 1 ( a , p ) = 1
a x ≡ b ( m o d p ) a^x \equiv b \pmod p
a x ≡ b ( m o d p )
考虑按 t t t
a i t + j ≡ b ( m o d p ) a^{it + j} \equiv b \pmod p
a i t + j ≡ b ( m o d p )
移一下项也就是:
a j ≡ b × a − i t ( m o d p ) a^j \equiv b \times a^{-it} \pmod p
a j ≡ b × a − i t ( m o d p )
所以就可以直接预处理 a 0 , a 1 , ⋯ , a t − 1 a^0,a^1,\cdots,a^{t-1} a 0 , a 1 , ⋯ , a t − 1 i i i b × a − i t b \times a^{-it} b × a − i t t = p t = \sqrt{p} t = p O ( p ) O(\sqrt{p}) O ( p )
不满足 ( a , p ) = 1 (a,p) = 1 ( a , p ) = 1
a x ≡ b ( m o d p ) a^x \equiv b \pmod p
a x ≡ b ( m o d p )
想法就是将这个方程转化为 ( a , p ) = 1 (a,p) = 1 ( a , p ) = 1
a x + k p = b a^x + kp = b
a x + k p = b
设 ( a , p ) = d (a,p) = d ( a , p ) = d d ∣ b d \mid b d ∣ b
a x − 1 ⋅ a d + k ⋅ p d = b d a^{x-1}\cdot \frac{a}{d} + k\cdot \frac{p}{d} = \frac{b}{d}
a x − 1 ⋅ d a + k ⋅ d p = d b
此时可以令 a x − 1 → a x , p d → p , b d → b a^{x-1} \to a^x,\frac{p}{d} \to p,\frac{b}{d} \to b a x − 1 → a x , d p → p , d b → b ( a , p ) = 1 (a,p) = 1 ( a , p ) = 1 c n t cnt c n t d d d d ′ d' d ′
a x − c n t ⋅ a c n t d ′ ≡ b d ′ ( m o d p d ′ ) a^{x-cnt}\cdot \frac{a^{cnt}}{d'} \equiv \frac{b}{d'} \pmod{\frac{p}{d'}}
a x − c n t ⋅ d ′ a c n t ≡ d ′ b ( m o d d ′ p )
此时直接令 a ′ = a , b ′ = b d ′ , p ′ = p d ′ a' = a,b' = \frac{b}{d'},p'= \frac{p}{d'} a ′ = a , b ′ = d ′ b , p ′ = d ′ p c n t cnt c n t a c n t d ′ \frac{a_{cnt}}{d'} d ′ a c n t
定义: p p p ( n , p ) = 1 (n,p) = 1 ( n , p ) = 1 x x x
x 2 ≡ n ( m o d p ) x^2 \equiv n \pmod p
x 2 ≡ n ( m o d p )
则称 n n n p p p n ≥ 1 n \ge 1 n ≥ 1
二次剩余的数量: n n n x 2 ≡ n ( m o d p ) x^2 \equiv n \pmod p x 2 ≡ n ( m o d p ) x 0 , x 1 x_0,x_1 x 0 , x 1 x 0 ≠ x 1 x_0 \not= x_1 x 0 = x 1
x 0 2 ≡ x 1 2 ( m o d p ) x_0^2 \equiv x_1^2 \pmod p
x 0 2 ≡ x 1 2 ( m o d p )
化简一下就是:
( x 0 − x 1 ) ( x 0 + x 1 ) ≡ 0 ( m o d p ) (x_0-x_1)(x_0+x_1) \equiv 0 \pmod p
( x 0 − x 1 ) ( x 0 + x 1 ) ≡ 0 ( m o d p )
因为 x 0 ≠ x 1 x_0 \not= x_1 x 0 = x 1 x 0 − x 1 ≠ 0 x_0 - x_1 \not= 0 x 0 − x 1 = 0 0 0 0 x 0 + x 1 = 0 ( m o d p ) x_0 + x_1 = 0\pmod p x 0 + x 1 = 0 ( m o d p ) p p p p p p x 0 , x 1 x_0,x_1 x 0 , x 1 x 0 + x 1 = 0 x_0 + x_1 = 0 x 0 + x 1 = 0 x 0 ≠ x 1 x_0 \not= x_1 x 0 = x 1 p − 1 2 \frac{p-1}{2} 2 p − 1 p − 1 2 \frac{p-1}{2} 2 p − 1
欧拉准则: n n n n p − 1 ≡ 1 ( m o d p ) n^{p-1} \equiv 1 \pmod p n p − 1 ≡ 1 ( m o d p ) p p p n 2 ⋅ p − 1 2 ≡ 1 ( m o d p ) n^{2\cdot \frac{p-1}{2} } \equiv 1 \pmod p n 2 ⋅ 2 p − 1 ≡ 1 ( m o d p ) n p − 1 2 n^{\frac{p-1}{2}} n 2 p − 1 1 1 1 1 1 1 1 1 1 − 1 -1 − 1 n p − 1 2 n^{\frac{p-1}{2}} n 2 p − 1 1 1 1 − 1 -1 − 1
下面考虑证明 n p − 1 2 ≡ 1 ( m o d p ) n^{\frac{p-1}{2}} \equiv 1 \pmod p n 2 p − 1 ≡ 1 ( m o d p ) n n n
充分性,也就是已知 n p − 1 2 ≡ 1 ( m o d p ) n^{\frac{p-1}{2}} \equiv 1 \pmod p n 2 p − 1 ≡ 1 ( m o d p ) g g g p p p n = g k n = g^k n = g k g k ⋅ p − 1 2 ≡ 1 ( m o d p ) g^{k\cdot \frac{p-1}{2}} \equiv 1 \pmod p g k ⋅ 2 p − 1 ≡ 1 ( m o d p ) ( p − 1 ) ∣ k ⋅ p − 1 2 (p-1) \mid k\cdot \frac{p-1}{2} ( p − 1 ) ∣ k ⋅ 2 p − 1 k k k k k k 2 2 2 n n n x = g k 2 x = g^{\frac{k}{2}} x = g 2 k
必要性,也就是已知 n n n n p − 1 2 = ( x 2 ) p − 1 2 = x p − 1 n^{\frac{p-1}{2}} = (x^2)^{\frac{p-1}{2}} = x^{p-1} n 2 p − 1 = ( x 2 ) 2 p − 1 = x p − 1 x φ ( p ) ≡ 1 ( m o d p ) x^{\varphi(p)} \equiv 1 \pmod p x φ ( p ) ≡ 1 ( m o d p ) x p − 1 ≡ 1 ( m o d p ) x^{p-1} \equiv 1 \pmod p x p − 1 ≡ 1 ( m o d p ) n p − 1 2 ≡ 1 ( m o d p ) n^{\frac{p-1}{2}} \equiv 1 \pmod p n 2 p − 1 ≡ 1 ( m o d p )
所以就证明了 n p − 1 2 ≡ 1 ( m o d p ) n^{\frac{p-1}{2}} \equiv 1 \pmod p n 2 p − 1 ≡ 1 ( m o d p ) n n n n p − 1 2 ≡ − 1 ( m o d p ) n^{\frac{p-1}{2}} \equiv -1 \pmod p n 2 p − 1 ≡ − 1 ( m o d p ) n n n
Cipolla: x 2 ≡ n ( m o d p ) x^2 \equiv n \pmod p x 2 ≡ n ( m o d p ) a a a a 2 − n a^2 - n a 2 − n p 2 \frac{p}{2} 2 p i 2 = a 2 − n i^2 = a^2 - n i 2 = a 2 − n i i i i i i A + B i A + Bi A + B i A , B A,B A , B p p p
( a + i ) p + 1 ≡ n ( m o d p ) (a+i)^{p+1} \equiv n \pmod p
( a + i ) p + 1 ≡ n ( m o d p )
引理 1 1 1 i p ≡ − i ( m o d p ) i^p \equiv -i \pmod p i p ≡ − i ( m o d p )
证明:i p = i ( i 2 ) p − 1 2 = i ( a 2 − n ) p − 1 2 = − i i^p = i(i^2)^{\frac{p-1}{2}} = i(a^2 - n)^{\frac{p-1}{2}} = -i i p = i ( i 2 ) 2 p − 1 = i ( a 2 − n ) 2 p − 1 = − i
引理 2 2 2 ( A + B ) p ≡ A p + B p ( m o d p ) (A+B)^p \equiv A^p + B^p \pmod p ( A + B ) p ≡ A p + B p ( m o d p )
证明:( A + B ) p ≡ ∑ i = 0 p ( p i ) A i B p − i ≡ ( p p ) A p + ( p 0 ) B p ≡ A p + B p ( m o d p ) (A+B)^p \equiv \sum_{i=0}^p \binom{p}{i} A^iB^{p-i} \equiv \binom{p}{p} A^p + \binom{p}{0}B^p \equiv A^p + B^p \pmod p ( A + B ) p ≡ ∑ i = 0 p ( i p ) A i B p − i ≡ ( p p ) A p + ( 0 p ) B p ≡ A p + B p ( m o d p )
有了这两个引理就可以证明了:
( a + i ) p + 1 ≡ ( a p + i p ) ( a + i ) ≡ ( a − i ) ( a + i ) ≡ a 2 − i 2 ≡ n ( m o d p ) (a+i)^{p+1} \equiv (a^p + i^p)(a+i) \equiv (a-i)(a+i) \equiv a^2 - i^2 \equiv n \pmod p
( a + i ) p + 1 ≡ ( a p + i p ) ( a + i ) ≡ ( a − i ) ( a + i ) ≡ a 2 − i 2 ≡ n ( m o d p )
第二个等于号 a p ≡ a ( m o d p ) a^p \equiv a \pmod p a p ≡ a ( m o d p )
因为 p p p p + 1 p+1 p + 1 n n n ( a + i ) p + 1 2 (a+i)^{\frac{p+1}{2}} ( a + i ) 2 p + 1 x x x ( a + i ) p + 1 2 (a+i)^{\frac{p+1}{2}} ( a + i ) 2 p + 1
可以证明 ( a + i ) p + 1 2 (a+i)^{\frac{p+1}{2}} ( a + i ) 2 p + 1 0 0 0
使用反证法来证明这个结论,若存在 ( A + B i ) 2 ≡ n ( m o d p ) (A+Bi)^2 \equiv n \pmod p ( A + B i ) 2 ≡ n ( m o d p ) B ≠ 0 B \not= 0 B = 0 A 2 + B 2 i 2 + 2 A B i ≡ n ( m o d p ) A^2 + B^2i^2 + 2ABi \equiv n \pmod p A 2 + B 2 i 2 + 2 A B i ≡ n ( m o d p ) 0 0 0 0 0 0 A B = 0 AB = 0 A B = 0 B ≠ 0 B \not= 0 B = 0 A = 0 A = 0 A = 0 B 2 i 2 ≡ n ( m o d p ) B^2i^2 \equiv n \pmod p B 2 i 2 ≡ n ( m o d p ) i 2 ≡ n B − 2 ( m o d p ) i^2 \equiv nB^{-2} \pmod p i 2 ≡ n B − 2 ( m o d p ) B − 2 B^{-2} B − 2 n n n n B − 2 nB^{-2} n B − 2 i 2 i^2 i 2 i 2 i^2 i 2
内容: 对于任意一个大于 1 1 1 N N N 标准分解式: N = ∏ i = 1 m p i k i N = \prod_{i=1}^m p_i^{k_i} N = ∏ i = 1 m p i k i p 1 < p 2 < p 3 ⋯ < p m p_1 < p_2 < p_3 \cdots < p_m p 1 < p 2 < p 3 ⋯ < p m p 1 , p 2 , p 3 , ⋯ , p m p_1,p_2,p_3,\cdots,p_m p 1 , p 2 , p 3 , ⋯ , p m k i k_i k i N N N p 进赋值序列: 记 v p ( n ) = max { k ∈ n ∣ p k ∣ n } v_p(n) = \max\{k \in \mathbb{n}\mid p^k \mid n\} v p ( n ) = max { k ∈ n ∣ p k ∣ n } n n n p p p { v 2 ( n ) , v 3 ( n ) , v 5 ( n ) , v 7 ( n ) , ⋯ } \{v_2(n),v_3(n),v_5(n),v_7(n),\cdots\} { v 2 ( n ) , v 3 ( n ) , v 5 ( n ) , v 7 ( n ) , ⋯ } p p p
p p p p p p
gcd \gcd g cdlcm \text{lcm} lcm min \min min max \max max
狄利克雷前缀和就对应高维前缀和,狄利克雷卷积就对应着高维和卷积。
莫比乌斯函数相当于高维差分的容斥系数。
素性检测就是在不对给定数进行质因数分解的情况下判断这个数是否为质数。
引理一:费马小定理p p p a a a ( a , p ) = 1 (a,p) = 1 ( a , p ) = 1 a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \pmod p a p − 1 ≡ 1 ( m o d p ) p p p p p p p p p
引理二:二次检测定理p p p 0 < x < p 0 < x < p 0 < x < p x 2 ≡ 1 ( m o d p ) x^2 \equiv 1 \pmod p x 2 ≡ 1 ( m o d p ) x = 1 x=1 x = 1 x = p − 1 x=p-1 x = p − 1 x 2 ≡ 1 ( m o d p ) ⟹ x 2 − 1 ≡ 0 ( m o d p ) ⟹ ( x + 1 ) ( x − 1 ) ≡ 0 ( m o d p ) ⟹ p ∣ ( x + 1 ) ( x − 1 ) x^2 \equiv 1 \pmod p \Longrightarrow x^2 - 1 \equiv 0 \pmod p \Longrightarrow (x+1)(x-1) \equiv 0 \pmod p \Longrightarrow p \mid (x+1)(x-1) x 2 ≡ 1 ( m o d p ) ⟹ x 2 − 1 ≡ 0 ( m o d p ) ⟹ ( x + 1 ) ( x − 1 ) ≡ 0 ( m o d p ) ⟹ p ∣ ( x + 1 ) ( x − 1 ) p p p x = 1 x = 1 x = 1 x = p − 1 x = p-1 x = p − 1
下面考虑给定 p p p p − 1 p-1 p − 1 2 k × t 2^k \times t 2 k × t a a a a t ( m o d p ) a^t \pmod p a t ( m o d p ) A A A A × A = 1 A \times A = 1 A × A = 1 A ≠ 1 A \not= 1 A = 1 A ≠ p − 1 A \not= p-1 A = p − 1 p p p k k k a p − 1 a^{p-1} a p − 1 a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \pmod p a p − 1 ≡ 1 ( m o d p ) 12 12 1 2 a a a [ 1 , 2 64 ) [1,2^{64}) [ 1 , 2 6 4 ) O ( ∣ a ∣ l o g 3 n ) O(|a|log^3n) O ( ∣ a ∣ l o g 3 n )
代码实现如下:
点击查看代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 bool Miller (int P) if (P == 1 ) return 0 ; int t = P - 1 , k = 0 ; while (!(t & 1 )) k++, t >>= 1 ; for (int i = 0 ; i < 12 ; i++) { if (P == Test[i]) return 1 ; LL a = pow (Test[i], t, P), nxt = a; for (int j = 1 ; j <= k; j++) { nxt = (a * a) % P; if (nxt == 1 && a != 1 && a != P - 1 ) return 0 ; a = nxt; } if (a != 1 ) return 0 ; } return 1 ; }
首先要明确这个算法的功能就是在 O ( n 1 4 ) O(n^{\frac{1}{4}}) O ( n 4 1 ) n n n
一个暴力的想法就是我们每次随机一个数,判断这个数是不是因子,如果是就返回如果不是就继续随机,但是这样的复杂度就炸了。f ( x ) = ( x 2 + c ) ( m o d N ) f(x) = (x^2 + c) \pmod N f ( x ) = ( x 2 + c ) ( m o d N ) x , f ( x ) , f ( f ( x ) ) , ⋯ x,f(x),f(f(x)),\cdots x , f ( x ) , f ( f ( x ) ) , ⋯
也就是一个 ρ \rho ρ O ( n 1 4 ) O(n^{\frac{1}{4}}) O ( n 4 1 ) O ( n 1 4 ) O(n^{\frac{1}{4}}) O ( n 4 1 ) t , r t,r t , r g c d ( ∣ t − r ∣ , n ) ≠ 1 gcd(|t-r|,n) \not= 1 g c d ( ∣ t − r ∣ , n ) = 1 g c d ( ∣ t − r ∣ , n ) ≠ n gcd(|t-r|,n) \not= n g c d ( ∣ t − r ∣ , n ) = n ∣ t − r ∣ |t-r| ∣ t − r ∣ n n n t = f ( t ) , r = f ( f ( r ) ) t = f(t),r=f(f(r)) t = f ( t ) , r = f ( f ( r ) ) r r r t t t ∣ i − j ∣ ≡ 0 ( m o d p ) |i-j| \equiv 0 \pmod p ∣ i − j ∣ ≡ 0 ( m o d p ) ∣ f i − f j ∣ = ( i 2 − j 2 ) = ( i − j ) ( i + j ) ≡ 0 ( m o d p ) |f_i - f_j| = (i^2 - j^2) = (i-j)(i+j) \equiv 0 \pmod p ∣ f i − f j ∣ = ( i 2 − j 2 ) = ( i − j ) ( i + j ) ≡ 0 ( m o d p ) d d d O ( n 1 4 log n ) O(n^{\frac{1}{4}}\log n) O ( n 4 1 log n ) g c d gcd g c d C C C C C C O ( n 1 4 ) O(n^\frac{1}{4}) O ( n 4 1 )
代码实现:
点击查看代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 ll Pollard_Rho (ll N) if (N == 4 ) return 2 ; if (is_prime (N)) return N; while (1 ) { ll c = randint (1 , N - 1 ); auto f = [=](ll x) { return ((lll)x * x + c) % N; }; ll t = 0 , r = 0 , p = 1 , q; do { for (int i = 0 ; i < 128 ; ++i) { t = f (t), r = f (f (r)); if (t == r || (q = (lll)p * abs (t - r) % N) == 0 ) break ; p = q; } ll d = gcd (p, N); if (d > 1 ) return d; } while (t != r); } }
此处可以查看如下几篇 blog,推荐按顺序观看:
【学习笔记】数论入门基础 【学习笔记】欧拉函数 【学习笔记】莫比乌斯反演 【学习笔记】数论之筛法
本文只在此基础上补充几个知识点。
给定区间 [ l , r ] [l,r] [ l , r ] [ l , r ] [l,r] [ l , r ] x ≤ r x \le r x ≤ r x x x x x x r \sqrt{r} r [ 2 , r ] [2,\sqrt{r}] [ 2 , r ] [ l , r ] [l,r] [ l , r ]
a m o d b = a − a × ⌊ a b ⌋ a \mod b = a - a\times \lfloor \frac{a}{b} \rfloor a m o d b = a − a × ⌊ b a ⌋
⌊ ⌊ a b ⌋ c ⌋ = ⌊ a b c ⌋ \lfloor {\frac{\lfloor\frac{a}{b}\rfloor}{c}} \rfloor = \lfloor {\frac{a}{bc}} \rfloor ⌊ c ⌊ b a ⌋ ⌋ = ⌊ b c a ⌋
整除分块中如果式子中多个数整除,复杂度是加而不是乘。
FWT 与 FMT 是解决如下问题的工具:
c k = ∑ i ⊕ j = k a i b j c_k = \sum_{i\oplus j = k}a_ib_j
c k = i ⊕ j = k ∑ a i b j
其中 ⊕ \oplus ⊕ and or xor 三种运算之一。a , b a,b a , b FWT ( a ) , FWT ( b ) \text{FWT}(a),\text{FWT}(b) FWT ( a ) , FWT ( b ) FWT ( c ) \text{FWT}(c) FWT ( c ) c c c
要求:
c k = ∑ i ∣ j = k a i b j c_k = \sum_{i | j = k} a_ib_j
c k = i ∣ j = k ∑ a i b j
考虑若 i ∣ k = k i \mid k = k i ∣ k = k j ∣ k = k j \mid k = k j ∣ k = k ( i ∣ j ) ∣ k = k (i\mid j) \mid k = k ( i ∣ j ) ∣ k = k FWT o r ( A ) k = ∑ i ∣ k = k A i \text{FWT}_{or}(A)_k = \sum_{i\mid k = k} A_i FWT o r ( A ) k = ∑ i ∣ k = k A i i i i k k k
FWT o r ( A ) = ∑ k ( ∑ i ∣ k = k A i ) × ( ∑ j ∣ k = k B j ) = ∑ k ∑ i ∣ k = k ∑ j ∣ k = k A i B j = ∑ k ∑ ( i ∣ j ) ∣ k = k A i B j \begin{aligned}
\text{FWT}_{or}(A) &= \sum_{k} (\sum_{i \mid k = k}A_i) \times (\sum_{j \mid k = k} B_j) \\
&= \sum_{k} \sum_{i \mid k = k}\sum_{j \mid k = k} A_iB_j \\
&= \sum_{k} \sum_{(i \mid j) \mid k = k} A_iB_j
\end{aligned}
FWT o r ( A ) = k ∑ ( i ∣ k = k ∑ A i ) × ( j ∣ k = k ∑ B j ) = k ∑ i ∣ k = k ∑ j ∣ k = k ∑ A i B j = k ∑ ( i ∣ j ) ∣ k = k ∑ A i B j
所以这个变换就是正确的。2 n 2^n 2 n 1 1 1 A 1 A_1 A 1 0 0 0 A 0 A_0 A 0 o r or o r A 0 A_0 A 0 A 1 A_1 A 1 A 1 A_1 A 1 A 0 A_0 A 0
FWT o r ( A ) = ( FWT o r ( A 0 ) , FWT o r ( A 0 ) + FWT o r ( A 1 ) ) \text{FWT}_{or}(A) = (\text{FWT}_{or}(A_0),\text{FWT}_{or}(A_0) + \text{FWT}_{or}(A_1))
FWT o r ( A ) = ( FWT o r ( A 0 ) , FWT o r ( A 0 ) + FWT o r ( A 1 ) )
其中 A + B A + B A + B ( A , B ) (A,B) ( A , B ) A , B A,B A , B
IFWT o r ( A ) = ( IFWT o r ( A 0 ) , IFWT o r ( A 1 ) − IFWT o r ( A 0 ) ) \text{IFWT}_{or}(A) = (\text{IFWT}_{or}(A_0),\text{IFWT}_{or}(A_1) - \text{IFWT}_{or}(A_0))
IFWT o r ( A ) = ( IFWT o r ( A 0 ) , IFWT o r ( A 1 ) − IFWT o r ( A 0 ) )
代码:
点击查看代码
1 2 3 4 5 6 7 8 9 10 11 12 void Or (ll *x,int n,int op) for (int l=1 ;l<n;l<<=1 ){ for (int st=0 ;st<n;st+=l*2 ){ for (int i=0 ;i<l;i++){ ll u=x[st+i],v=x[st+l+i]; if (op==1 ) x[st+i]=u,x[st+l+i]=(v+u)%mod; else x[st+i]=u,x[st+l+i]=(v+mod-u)%mod; } } } }
要求:
c k = ∑ i & j = k a i b j c_k = \sum_{i \& j = k} a_ib_j
c k = i & j = k ∑ a i b j
考虑若 i & k = k i \& k = k i & k = k j & k = k j \& k = k j & k = k ( i & j ) & k = k (i\&j) \& k = k ( i & j ) & k = k FWT a n d ( A ) k = ∑ i & k = k A i \text{FWT}_{and}(A)_k = \sum_{i\&k=k} A_i FWT a n d ( A ) k = ∑ i & k = k A i i i i k k k
FWT a n d ( A ) = ( FWT a n d ( A 0 ) + FWT a n d ( A 1 ) , FWT a n d ( A 1 ) ) IFWT a n d ( A ) = ( IFWT a n d ( A 0 ) − IFWT a n d ( A 1 ) , IFWT a n d ( A 1 ) ) \text{FWT}_{and}(A) = (\text{FWT}_{and}(A_0)+\text{FWT}_{and}(A_1),\text{FWT}_{and}(A_1)) \\
\text{IFWT}_{and}(A) = (\text{IFWT}_{and}(A_0)-\text{IFWT}_{and}(A_1),\text{IFWT}_{and}(A_1))
FWT a n d ( A ) = ( FWT a n d ( A 0 ) + FWT a n d ( A 1 ) , FWT a n d ( A 1 ) ) IFWT a n d ( A ) = ( IFWT a n d ( A 0 ) − IFWT a n d ( A 1 ) , IFWT a n d ( A 1 ) )
代码:
点击查看代码
1 2 3 4 5 6 7 8 9 10 11 12 void And (ll *x,int n,int op) for (int l=1 ;l<n;l<<=1 ){ for (int st=0 ;st<n;st+=l*2 ){ for (int i=0 ;i<l;i++){ ll u=x[st+i],v=x[st+l+i]; if (op==1 ) x[st+i]=(u+v)%mod,x[st+l+i]=v; else x[st+i]=(u+mod-v)%mod,x[st+l+i]=v; } } } }
要求:
c k = ∑ i ⊕ j = k a i b j c_k = \sum_{i \oplus j = k} a_ib_j
c k = i ⊕ j = k ∑ a i b j
设 d ( x ) d(x) d ( x ) x x x 1 1 1 d ( i & k ) ⊕ d ( j & k ) = d ( ( i ⊕ j ) & k ) d(i\&k)\oplus d(j\&k) = d((i\oplus j) \& k) d ( i & k ) ⊕ d ( j & k ) = d ( ( i ⊕ j ) & k ) k k k 1 1 1 i , j i,j i , j 0 0 0 1 1 1 i , j i,j i , j 0 , 1 0,1 0 , 1
所以可以设计出以下的变换:
FWT x o r ( A ) k = ∑ i ( − 1 ) d ( i & k ) A i \text{FWT}_{xor}(A)_k = \sum_{i} (-1)^{d(i\&k)} A_i
FWT x o r ( A ) k = i ∑ ( − 1 ) d ( i & k ) A i
可以乘一下看看是不是对的:
FWT x o r ( C ) = ∑ k ( ∑ i ( − 1 ) d ( i & k ) A i ) ( ∑ j ( − 1 ) d ( j & k ) B j ) = ∑ k ∑ i ∑ j ( − 1 ) d ( i & k ) + d ( j & k ) A i B j = ∑ k ∑ i , j ( − 1 ) d ( i & k ) ⊕ d ( j & k ) A i B j = ∑ k ∑ i , j ( − 1 ) d ( ( i ⊕ j ) & k ) A i B j \begin{aligned}
\text{FWT}_{xor}(C) &= \sum_{k} (\sum_{i} (-1)^{d(i\&k)} A_i) (\sum_{j} (-1)^{d(j\&k)} B_j) \\
&= \sum_{k} \sum_{i} \sum_{j} (-1)^{d(i\&k) + d(j\&k)} A_iB_j \\
&= \sum_{k} \sum_{i,j} (-1)^{d(i\&k)\oplus d(j\&k)} A_iB_j \\
&= \sum_{k} \sum_{i,j} (-1)^{d((i\oplus j)\&k)} A_iB_j
\end{aligned}
FWT x o r ( C ) = k ∑ ( i ∑ ( − 1 ) d ( i & k ) A i ) ( j ∑ ( − 1 ) d ( j & k ) B j ) = k ∑ i ∑ j ∑ ( − 1 ) d ( i & k ) + d ( j & k ) A i B j = k ∑ i , j ∑ ( − 1 ) d ( i & k ) ⊕ d ( j & k ) A i B j = k ∑ i , j ∑ ( − 1 ) d ( ( i ⊕ j ) & k ) A i B j
这样就形式化对了,所以这个就是正确的。
考虑怎么快速求解,其实就是新加一位,而新加一位只有 1 1 1 1 1 1
FWT x o r ( A ) = ( FWT x o r ( A 0 ) + FWT x o r ( A 1 ) , FWT x o r ( A 0 ) − FWT x o r ( A 1 ) ) \text{FWT}_{xor}(A) = (\text{FWT}_{xor}(A_0) + \text{FWT}_{xor}(A_1),\text{FWT}_{xor}(A_0) - \text{FWT}_{xor}(A_1))
FWT x o r ( A ) = ( FWT x o r ( A 0 ) + FWT x o r ( A 1 ) , FWT x o r ( A 0 ) − FWT x o r ( A 1 ) )
逆变换其实就是考虑 A 0 , A 1 A_0,A_1 A 0 , A 1
IFWT x o r ( A ) = ( IFWT x o r ( A 0 ) + IFWT x o r ( A 1 ) 2 , IFWT x o r ( A 0 ) − IFWT x o r ( A 1 ) 2 ) \text{IFWT}_{xor}(A) = (\frac{\text{IFWT}_{xor}(A_0) + \text{IFWT}_{xor}(A_1)}{2},\frac{\text{IFWT}_{xor}(A_0) - \text{IFWT}_{xor}(A_1)}{2})
IFWT x o r ( A ) = ( 2 IFWT x o r ( A 0 ) + IFWT x o r ( A 1 ) , 2 IFWT x o r ( A 0 ) − IFWT x o r ( A 1 ) )
代码:
点击查看代码
1 2 3 4 5 6 7 8 9 10 11 void Xor (ll *x,int n,int op) for (int l=1 ;l<n;l<<=1 ){ for (int st=0 ;st<n;st+=l*2 ){ for (int i=0 ;i<l;i++){ ll u=x[st+i],v=x[st+l+i]; if (op==1 ) x[st+i]=(u+v)%mod,x[st+l+i]=(u+mod-v)%mod; else x[st+i]=(u+v)%mod*inv2%mod,x[st+l+i]=(u+mod-v)%mod*inv2%mod; } } } }
FWT 的本质是一个线性变换,也就是:FWT ( A + B ) = FWT ( A ) + FWT ( B ) \text{FWT}(A+B) = \text{FWT}(A) + \text{FWT}(B) FWT ( A + B ) = FWT ( A ) + FWT ( B ) FWT ( c A ) = c FWT ( A ) \text{FWT}(cA) = c\text{FWT}(A) FWT ( c A ) = c FWT ( A )
位运算是 OI 中的常考知识点,因为位运算中每一位的独立性,所以可以将其看作两个 { 0 , 1 } n \{0,1\}^n { 0 , 1 } n a 0 , a 1 , ⋯ , a 2 n − 1 a_0,a_1,\cdots,a_{2^n-1} a 0 , a 1 , ⋯ , a 2 n − 1 A ( x ) = ∑ i = 0 2 n − 1 a i x i A(x) = \sum \limits_{i=0}^{2^n-1}a_ix^i A ( x ) = i = 0 ∑ 2 n − 1 a i x i
定义集合幂级数的乘法操作,也就是子集卷积为如下的形式;
c i = ∑ j ∣ k = i j & k = 0 a j b k \begin{aligned}
c_i = \sum_{j \mid k = i \quad j \& k = 0} a_jb_k
\end{aligned}
c i = j ∣ k = i j & k = 0 ∑ a j b k
组合意义就是选择两个不交的集合,可以直接枚举子集就可以做到 O ( 3 n ) O(3^n) O ( 3 n ) w ( x ) = popcount ( x ) w(x) = \text{popcount}(x) w ( x ) = popcount ( x ) j xor k = i j \ \text{xor} \ k = i j xor k = i w ( j ) + w ( k ) = w ( i ) w(j) + w(k) = w(i) w ( j ) + w ( k ) = w ( i ) w ( x ) w(x) w ( x ) A ( x , y ) = ∑ i = 0 2 n − 1 a i x i y w ( i ) A(x,y) = \sum \limits_{i=0}^{2^n-1} a_ix^iy^{w(i)} A ( x , y ) = i = 0 ∑ 2 n − 1 a i x i y w ( i ) O ( n 2 2 n ) O(n^22^n) O ( n 2 2 n ) O ( log n ) O(\log n) O ( log n )
代码:
点击查看代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int main () m=read ();n=(1 <<m); for (int i=1 ;i<n;i++)c[i]=c[i>>1 ]+(i&1 ); for (int i=0 ;i<n;i++)F[i].a[c[i]]=read (); for (int i=0 ;i<n;i++)G[i].a[c[i]]=read (); FWT (F,n);FWT (G,n); for (int i=0 ;i<n;i++) F[i]=F[i]*G[i]; IFWT (F,n); for (int i=0 ;i<n;i++) printf ("%d " ,(F[i].a[c[i]]+mod)%mod); return 0 ; }
这个技巧就被称为占位多项式,有了这个占位多项式我们就可以对集合幂级数做各种多项式的操作,但是那东西我完全不会,就不说了。
加法原理: 若完成某道工序有两种方法,第一种方法的实现方式有 a a a b b b a + b a+b a + b 乘法原理: 若完成某道工序有两个步骤,第一个步骤有 a a a b b b a b ab a b 算两次原理(富比尼原理): 将同一个量同两个不同角度计算两次,从而建立等量关系。
例题 P8557 炼金术 :k k k n n n n n n
考虑按每一种金属考虑,其在每一个熔炉中都可以出现或者不出现,所以方案数为 2 2 2 k k k 2 k 2^k 2 k 2 k − 1 2^k-1 2 k − 1 ( 2 k − 1 ) n (2^k-1)^n ( 2 k − 1 ) n
鸽巢原理: n n n m m m ⌈ n m ⌉ \lceil \frac{n}{m} \rceil ⌈ m n ⌉
递推形式:( n m ) = ( n − 1 m ) + ( n − 1 m − 1 ) \binom{n}{m} = \binom{n-1}{m} + \binom{n-1}{m-1} ( m n ) = ( m n − 1 ) + ( m − 1 n − 1 ) ( n m ) = n ! m ! ( n − m ) ! = n m ‾ m ! \binom{n}{m} = \frac{n!}{m!(n-m)!} = \frac{n^{\underline{m}}}{m!} ( m n ) = m ! ( n − m ) ! n ! = m ! n m ( n m ) = ( n m o d p m m o d p ) × ( ⌊ n p ⌋ ⌊ m p ⌋ ) \binom{n}{m} = \binom{n \mod p}{m \mod p} \times \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor} ( m n ) = ( m m o d p n m o d p ) × ( ⌊ p m ⌋ ⌊ p n ⌋ )
组合恒等式:
吸收恒等式: ( n m ) = n m ( n − 1 m − 1 ) \binom{n}{m} = \frac{n}{m} \binom{n-1}{m-1} ( m n ) = m n ( m − 1 n − 1 ) m ( n m ) = n ( n − 1 m − 1 ) m\binom{n}{m} = n\binom{n-1}{m-1} m ( m n ) = n ( m − 1 n − 1 )
行求和:∑ i = 0 n ( n i ) = 2 n \sum_{i=0}^n \binom{n}{i} = 2^n ∑ i = 0 n ( i n ) = 2 n ( 1 + 1 ) n = ∑ i = 0 n ( n i ) = 2 n (1+1)^n = \sum_{i=0}^n \binom{n}{i} = 2^n ( 1 + 1 ) n = ∑ i = 0 n ( i n ) = 2 n
列求和:∑ i = n m ( i n ) = ( m + 1 n + 1 ) \sum_{i=n}^m \binom{i}{n} = \binom{m+1}{n+1} ∑ i = n m ( n i ) = ( n + 1 m + 1 ) ( n n ) + ( n + 1 n ) + ( n + 2 n ) + ⋯ + ( m n ) = ( n + 1 n + 1 ) + ( n + 1 n ) + ( n + 2 n ) + ⋯ + ( m n ) = ( n + 2 n + 1 ) + ( n + 2 n ) + ⋯ + ( m n ) = ( m n + 1 ) + ( m n ) = ( m + 1 n + 1 ) \binom{n}{n} + \binom{n+1}{n} + \binom{n+2}{n} + \cdots + \binom{m}{n} = \binom{n+1}{n+1} + \binom{n+1}{n} + \binom{n+2}{n} + \cdots + \binom{m}{n} = \binom{n+2}{n+1} + \binom{n+2}{n} + \cdots + \binom{m}{n} = \binom{m}{n+1} + \binom{m}{n} = \binom{m+1}{n+1} ( n n ) + ( n n + 1 ) + ( n n + 2 ) + ⋯ + ( n m ) = ( n + 1 n + 1 ) + ( n n + 1 ) + ( n n + 2 ) + ⋯ + ( n m ) = ( n + 1 n + 2 ) + ( n n + 2 ) + ⋯ + ( n m ) = ( n + 1 m ) + ( n m ) = ( n + 1 m + 1 )
范德蒙德卷积:∑ i = 0 k ( n i ) × ( m k − i ) = ( n + m k ) \sum_{i=0}^k \binom{n}{i}\times\binom{m}{k-i} = \binom{n+m}{k} ∑ i = 0 k ( i n ) × ( k − i m ) = ( k n + m ) n n n i i i m m m k − i k-i k − i
隔板法:n n n m m m ( n − 1 m − 1 ) \binom{n-1}{m-1} ( m − 1 n − 1 ) n n n n − 1 n-1 n − 1 k k k k k k k − 1 k-1 k − 1 ( n − 1 m − 1 ) \binom{n-1}{m-1} ( m − 1 n − 1 ) ( n + m − 1 m − 1 ) \binom{n+m-1}{m-1} ( m − 1 n + m − 1 ) 1 1 1
捆绑法:有 n n n ( n − 1 ) ! × 2 ! (n-1)! \times 2! ( n − 1 ) ! × 2 ! ( n − 1 ) ! (n-1)! ( n − 1 ) ! 2 ! 2! 2 !
格路计数:给定一个 n × m n \times m n × m ( x , y ) (x,y) ( x , y ) ( x + 1 , y ) (x+1,y) ( x + 1 , y ) ( x , y + 1 ) (x,y+1) ( x , y + 1 ) ( 1 , 1 ) (1,1) ( 1 , 1 ) ( n , m ) (n,m) ( n , m ) ( n + m n ) \binom{n+m}{n} ( n n + m ) n + m n+m n + m ( n , m ) (n,m) ( n , m ) n n n ( x , y ) → ( x + 1 , y ) (x,y) \to (x+1,y) ( x , y ) → ( x + 1 , y ) n n n
卡特兰数:见数论之生成函数基础。
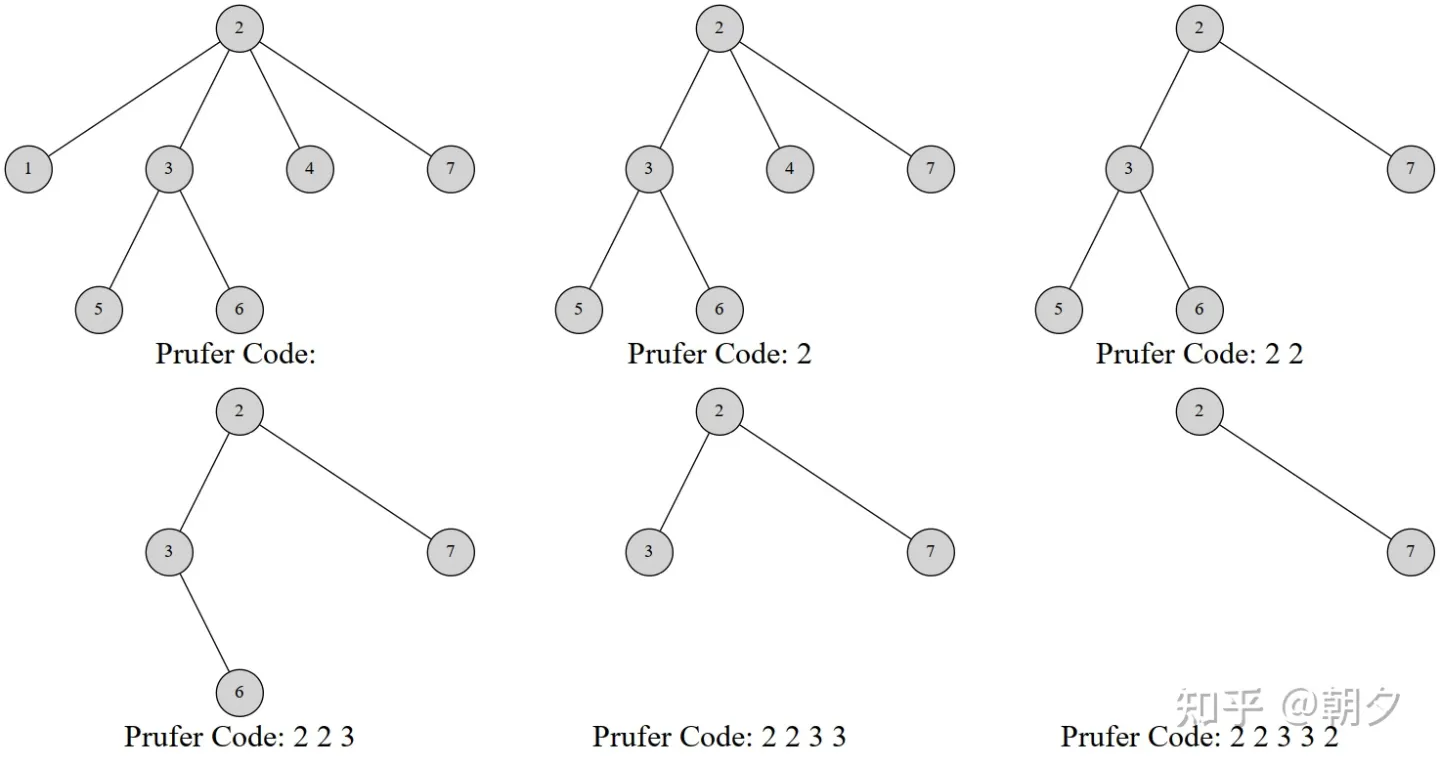
对于一棵有 n n n n − 2 n-2 n − 2 [ 1 , n ] [1,n] [ 1 , n ]
树转化为 prufer 序列:
选择树上编号最小的叶子节点,将其父亲插入到序列的末尾
删除这个选择的叶子节点
重复上述步骤直到树中只剩下两个节点
注意到我们的 prufer 序列与树构成一个双射,所以我们可以由 prufer 序列还原对应的树。
选择编号最小的一个叶子节点(即从未在序列中出现的点),其父亲就是序列第 i i i i i i 1 1 1
点 x x x x x x 1 1 1 1 1 1 1 1 1
重复上述两步,直到序列全部被用完。
可以发现这样构造出的 prufer 序列有如下的性质:
剩下的两个节点中,一定有一个为 n n n
对于一个 n n n n − 1 n-1 n − 1
应用:
无向完全图生成树计数:若该完全图点数为 n n n n − 2 n-2 n − 2 [ 1 , n ] [1,n] [ 1 , n ] n n − 2 n^{n-2} n n − 2
Cayley 定理:假设图中有 m m m a 1 , a 2 , ⋯ , a m a_1,a_2,\cdots,a_m a 1 , a 2 , ⋯ , a m a 1 + a 2 + ⋯ + a m = n a_1 + a_2 + \cdots + a_m = n a 1 + a 2 + ⋯ + a m = n m − 1 m-1 m − 1 n m − 2 ∏ i = 1 m a i n^{m-2}\prod_{i=1}^m a_i n m − 2 ∏ i = 1 m a i
广义 Cayley 定理:n n n k k k k k k k × n n − k − 1 k \times n^{n-k-1} k × n n − k − 1
证明:k k k I I I I I I k k k I I I n + 1 n+1 n + 1 I = n + 1 I = n + 1 I = n + 1 k k k n − k + 1 , n − k + 2 , ⋯ , n n-k+1,n-k+2,\cdots,n n − k + 1 , n − k + 2 , ⋯ , n I I I k k k k k k k − 1 k-1 k − 1 n + 1 n+1 n + 1 k k k k k k n − k − 1 n-k-1 n − k − 1 k × n n − k − 1 k \times n^{n-k-1} k × n n − k − 1
n n n n × n n − 2 = n n − 1 n \times n^{n-2} = n^{n-1} n × n n − 2 = n n − 1
最基本的式子就是交集与并集的转化:S S S A i ⊆ S ( i ∈ [ 1 , n ] ) A_i \subseteq S(i \in [1,n]) A i ⊆ S ( i ∈ [ 1 , n ] )
∣ ⋃ i = 1 n A i ∣ = ∑ T ⊆ [ 1 , n ] ( − 1 ) ∣ T ∣ − 1 ∣ ⋂ j ∈ T A j ∣ = ∑ k = 1 n ( − 1 ) k − 1 ∑ b 1 < b 2 < b 3 < ⋯ < b k ∣ ⋂ j = 1 k A b j ∣ \left| \bigcup\limits_{i=1}^n A_i \right| = \sum_{T \subseteq [1,n]} (-1)^{|T|-1} \left| \bigcap\limits_{j \in T} A_j \right| = \sum_{k=1}^{n} (-1)^{k-1} \sum_{b_1 < b_2 < b_3 < \cdots < b_k} \left| \bigcap\limits_{j=1}^k A_{b_j} \right|
∣ ∣ ∣ ∣ ∣ ∣ i = 1 ⋃ n A i ∣ ∣ ∣ ∣ ∣ ∣ = T ⊆ [ 1 , n ] ∑ ( − 1 ) ∣ T ∣ − 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ j ∈ T ⋂ A j ∣ ∣ ∣ ∣ ∣ ∣ ∣ = k = 1 ∑ n ( − 1 ) k − 1 b 1 < b 2 < b 3 < ⋯ < b k ∑ ∣ ∣ ∣ ∣ ∣ ∣ j = 1 ⋂ k A b j ∣ ∣ ∣ ∣ ∣ ∣
证明:考虑元素 x x x m m m A A A ∑ i = 1 m ( − 1 ) i − 1 ( m i ) = − ( ∑ i = 1 m ( − 1 ) i ( m i ) ) = − ( − 1 + ∑ i = 0 m ( − 1 ) i ( m i ) ) = − ( − 1 + ( 1 − 1 ) m ) = 1 \sum_{i=1}^m (-1)^{i-1} \binom{m}{i} = -(\sum_{i=1}^m (-1)^i \binom{m}{i}) = -(-1 + \sum_{i=0}^m (-1)^i \binom{m}{i}) = -(-1 + (1-1)^m) = 1 ∑ i = 1 m ( − 1 ) i − 1 ( i m ) = − ( ∑ i = 1 m ( − 1 ) i ( i m ) ) = − ( − 1 + ∑ i = 0 m ( − 1 ) i ( i m ) ) = − ( − 1 + ( 1 − 1 ) m ) = 1 A 1 A_1 A 1 A 2 A_2 A 2 ⋯ \cdots ⋯
当然有的时候也要有一些直观的理解,比如 [ a , b ] [a,b] [ a , b ] A A A [ 1 , b ] [1,b] [ 1 , b ] [ 1 , a − 1 ] [1,a-1] [ 1 , a − 1 ] A A A A A A
在容斥以及反演过程中常使用二项式定理证明结论。
反演其实就是容斥原理的代数形式,下面就简单介绍几种反演。
形式一:
F ( n ) = ∑ i = 0 n ( − 1 ) i ( n i ) G ( i ) ⟺ G ( n ) = ∑ i = 0 n ( − 1 ) i ( n i ) F ( i ) F(n) = \sum_{i=0}^n (-1)^i \binom{n}{i} G(i) \iff G(n) = \sum_{i=0}^n (-1)^i \binom{n}{i} F(i)
F ( n ) = i = 0 ∑ n ( − 1 ) i ( i n ) G ( i ) ⟺ G ( n ) = i = 0 ∑ n ( − 1 ) i ( i n ) F ( i )
证明:G ( n ) G(n) G ( n ) G ( i ) G(i) G ( i ) G ( n ) G(n) G ( n ) 1 1 1 0 0 0 G ( i ) G(i) G ( i ) F ( j ) F(j) F ( j ) F ( j ) F(j) F ( j ) G ( i ) G(i) G ( i )
a n s = ∑ j = i n ( − 1 ) j ( n j ) ( − 1 ) i ( j i ) = ( − 1 ) i ∑ j = i n ( − 1 ) j n ! j ! j ! ( n − j ) ! i ! ( j − i ) ! = ( − 1 ) i ∑ j = i n ( − 1 ) j n ! i ! ( n − i ! ) × ( n − i ) ! ( n − j ) ! ( j − i ) ! = ( − 1 ) i ( n i ) ∑ j = i n ( − 1 ) j ( n − i n − j ) = ( − 1 ) i ( n i ) ∑ j = 0 n − i ( − 1 ) j + 1 ( n − j n − j − i ) = ( − 1 ) 2 i ( n i ) ∑ j = 0 n − i ( − 1 ) j ( n − i j ) = ( − 1 ) 2 i ( n i ) ( 1 − 1 ) n − i = [ n = i ] \begin{aligned}
ans
&= \sum_{j=i}^n (-1)^j \binom{n}{j} (-1)^i \binom{j}{i} \\
&= (-1)^i \sum_{j=i}^n (-1)^j \frac{n!j!}{j!(n-j)!i!(j-i)!} \\
&= (-1)^i \sum_{j=i}^n (-1)^j \frac{n!}{i!(n-i!)} \times \frac{(n-i)!}{(n-j)!(j-i)!} \\
&= (-1)^i \binom{n}{i} \sum_{j=i}^n (-1)^j \binom{n-i}{n-j} \\
&= (-1)^i \binom{n}{i} \sum_{j=0}^{n-i} (-1)^{j+1} \binom{n-j}{n-j-i} \\
&= (-1)^{2i} \binom{n}{i} \sum_{j=0}^{n-i} (-1)^j \binom{n-i}{j} \\
&= (-1)^{2i} \binom{n}{i} (1-1)^{n-i} \\
&= [n = i]
\end{aligned}
a n s = j = i ∑ n ( − 1 ) j ( j n ) ( − 1 ) i ( i j ) = ( − 1 ) i j = i ∑ n ( − 1 ) j j ! ( n − j ) ! i ! ( j − i ) ! n ! j ! = ( − 1 ) i j = i ∑ n ( − 1 ) j i ! ( n − i ! ) n ! × ( n − j ) ! ( j − i ) ! ( n − i ) ! = ( − 1 ) i ( i n ) j = i ∑ n ( − 1 ) j ( n − j n − i ) = ( − 1 ) i ( i n ) j = 0 ∑ n − i ( − 1 ) j + 1 ( n − j − i n − j ) = ( − 1 ) 2 i ( i n ) j = 0 ∑ n − i ( − 1 ) j ( j n − i ) = ( − 1 ) 2 i ( i n ) ( 1 − 1 ) n − i = [ n = i ]
所以系数就正确了,得证。
形式二:
F ( n ) = ∑ i = 0 n ( n i ) G ( i ) ⟺ G ( n ) = ∑ i = 0 n ( − 1 ) n − i ( n i ) F ( i ) F(n) = \sum_{i=0}^n \binom{n}{i} G(i) \iff G(n) = \sum_{i=0}^n (-1)^{n-i} \binom{n}{i}F(i)
F ( n ) = i = 0 ∑ n ( i n ) G ( i ) ⟺ G ( n ) = i = 0 ∑ n ( − 1 ) n − i ( i n ) F ( i )
证明:
F ( n ) = ∑ i = 0 n n ! ( n − i ) ! i ! G ( i ) F ( n ) n ! = ∑ i = 0 n 1 ( n − i ) ! G ( i ) i ! F(n) = \sum_{i=0}^n \frac{n!}{(n-i)!i!}G(i) \\
\frac{F(n)}{n!} = \sum_{i=0}^n \frac{1}{(n-i)!} \frac{G(i)}{i!}
F ( n ) = i = 0 ∑ n ( n − i ) ! i ! n ! G ( i ) n ! F ( n ) = i = 0 ∑ n ( n − i ) ! 1 i ! G ( i )
这个式子显然就是一个卷积的形式也就是:
F = G ∗ e x ⟺ G = F ∗ e − x F = G * e^x \iff G = F * e^{-x}
F = G ∗ e x ⟺ G = F ∗ e − x
所以:
G ( n ) n ! = ∑ i = 0 n ( − 1 ) n − i ( n − i ) ! F ( i ) i ! \frac{G(n)}{n!} = \sum_{i=0}^n \frac{(-1)^{n-i}}{(n-i)!} \frac{F(i)}{i!}
n ! G ( n ) = i = 0 ∑ n ( n − i ) ! ( − 1 ) n − i i ! F ( i )
移项之后就是:
G ( n ) = ∑ i = 0 n ( − 1 ) n − i ( n i ) F ( i ) G(n) = \sum_{i=0}^n (-1)^{n-i} \binom{n}{i} F(i)
G ( n ) = i = 0 ∑ n ( − 1 ) n − i ( i n ) F ( i )
得证。
形式三:
F ( n ) = ∑ i = n ( i n ) G ( i ) ⟺ G ( n ) = ∑ i = n ( − 1 ) i − n ( i n ) F ( i ) F(n) = \sum_{i=n} \binom{i}{n} G(i) \iff G(n) = \sum_{i=n} (-1)^{i-n} \binom{i}{n} F(i)
F ( n ) = i = n ∑ ( n i ) G ( i ) ⟺ G ( n ) = i = n ∑ ( − 1 ) i − n ( n i ) F ( i )
形式四:
F ( n ) = ∑ i = n ( − 1 ) i ( i n ) G ( i ) ⟺ G ( n ) = ∑ i = n ( − 1 ) i ( i n ) F ( i ) F(n) = \sum_{i=n} (-1)^i \binom{i}{n} G(i) \iff G(n) = \sum_{i=n} (-1)^i \binom{i}{n} F(i)
F ( n ) = i = n ∑ ( − 1 ) i ( n i ) G ( i ) ⟺ G ( n ) = i = n ∑ ( − 1 ) i ( n i ) F ( i )
这两种形式都可以通过慢慢推的方式证明,因为形式一已经类似证明过了就不证明了。
请查看:
【学习笔记】数论入门基础 【学习笔记】莫比乌斯反演
定义全集 U = { a 1 , a 2 , a 3 , ⋯ , a n } U = \{a_1,a_2,a_3,\cdots,a_n\} U = { a 1 , a 2 , a 3 , ⋯ , a n } S S S max ( S ) = max a i ∈ S a i \max(S) = \max \limits_{a_i \in S} a_i max ( S ) = a i ∈ S max a i min ( S ) = min a i ∈ S a i \min(S) = \min \limits_{a_i\in S} a_i min ( S ) = a i ∈ S min a i
max ( S ) = ∑ T ⊆ S ( − 1 ) ∣ T ∣ + 1 min ( T ) min ( S ) = ∑ T ⊆ S ( − 1 ) ∣ T ∣ + 1 max ( T ) \max(S) = \sum_{T \subseteq S} (-1)^{|T|+1} \min(T) \\
\min(S) = \sum_{T \subseteq S} (-1)^{|T|+1} \max(T)
max ( S ) = T ⊆ S ∑ ( − 1 ) ∣ T ∣ + 1 min ( T ) min ( S ) = T ⊆ S ∑ ( − 1 ) ∣ T ∣ + 1 max ( T )
下面考虑证明第一个式子。x x x k k k x x x x x x
= ∑ i = 0 k − 1 ( k − 1 i ) ( − 1 ) i + 2 = ∑ i = 0 k − 1 ( k − 1 i ) ( − 1 ) i = ( 1 − 1 ) k − 1 = [ k = 1 ] \begin{aligned}
&= \sum_{i=0}^{k-1} \binom{k-1}{i} (-1)^{i+2} \\
&= \sum_{i=0}^{k-1} \binom{k-1}{i} (-1)^i \\
&= (1-1)^{k-1} \\
&= [k=1]
\end{aligned}
= i = 0 ∑ k − 1 ( i k − 1 ) ( − 1 ) i + 2 = i = 0 ∑ k − 1 ( i k − 1 ) ( − 1 ) i = ( 1 − 1 ) k − 1 = [ k = 1 ]
所以只有最大值会产生 1 1 1 0 0 0
要注意的一点就是 Min-Max 容斥在期望意义下依然成立,即:
E ( max ( S ) ) = ∑ T ⊆ S ( − 1 ) ∣ T ∣ + 1 min ( T ) E(\max(S)) = \sum_{T \subseteq S} (-1)^{|T|+1} \min(T)
E ( max ( S ) ) = T ⊆ S ∑ ( − 1 ) ∣ T ∣ + 1 min ( T )
如果我们要求第 k k k
K t h max ( S ) = ∑ T ⊆ S ( − 1 ) ∣ T ∣ − k ( ∣ T ∣ − 1 k − 1 ) min ( T ) K_{th}\max(S) = \sum_{T \subseteq S} (-1)^{|T| - k} \binom{|T|-1}{k-1} \min(T)
K t h max ( S ) = T ⊆ S ∑ ( − 1 ) ∣ T ∣ − k ( k − 1 ∣ T ∣ − 1 ) min ( T )
这个容斥系数我们是可以很简单推导出来的。
K t h max ( S ) = ∑ T ⊆ S F ( ∣ T ∣ ) min ( T ) K_{th}\max(S) = \sum_{T \subseteq S} F(|T|) \min(T)
K t h max ( S ) = T ⊆ S ∑ F ( ∣ T ∣ ) min ( T )
考虑若 x x x p p p
∑ i = 0 p − 1 ( p − 1 i ) F ( i + 1 ) \sum_{i=0}^{p-1} \binom{p-1}{i} F(i+1)
i = 0 ∑ p − 1 ( i p − 1 ) F ( i + 1 )
我们的目的就要让这个式子的值等于 [ p = k ] [p=k] [ p = k ]
∑ i = 0 p ( p i ) F ( i + 1 ) = [ p = k − 1 ] \sum_{i=0}^{p} \binom{p}{i} F(i+1) = [p=k-1]
i = 0 ∑ p ( i p ) F ( i + 1 ) = [ p = k − 1 ]
这个就是一个二项式反演的形式,所以就有:
F ( p + 1 ) = ∑ i = 0 p ( − 1 ) p − i ( p i ) [ i = k − 1 ] = ( − 1 ) p − k + 1 ( p k − 1 ) F(p+1) = \sum_{i=0}^p (-1)^{p-i} \binom{p}{i} [i=k-1] = (-1)^{p-k+1} \binom{p}{k-1}
F ( p + 1 ) = i = 0 ∑ p ( − 1 ) p − i ( i p ) [ i = k − 1 ] = ( − 1 ) p − k + 1 ( k − 1 p )
因此 F ( ∣ T ∣ ) = ( − 1 ) ∣ T ∣ − k ( ∣ T ∣ − 1 k − 1 ) F(|T|) = (-1)^{|T|-k}\binom{|T|-1}{k-1} F ( ∣ T ∣ ) = ( − 1 ) ∣ T ∣ − k ( k − 1 ∣ T ∣ − 1 )
莫比乌斯反演相当于在因子多重集上的子集反演,所以本质也是子集反演。A A A f ( S ) f(S) f ( S ) A = S A=S A = S g ( S ) g(S) g ( S ) S ⊆ A S \subseteq A S ⊆ A
g ( S ) = ∑ T ⊆ S f ( T ) ⟺ f ( S ) = ∑ T ⊆ S ( − 1 ) ∣ S ∣ − ∣ T ∣ g ( T ) g(S) = \sum_{T \subseteq S} f(T) \iff f(S) = \sum_{T \subseteq S} (-1)^{|S|-|T|}g(T)
g ( S ) = T ⊆ S ∑ f ( T ) ⟺ f ( S ) = T ⊆ S ∑ ( − 1 ) ∣ S ∣ − ∣ T ∣ g ( T )
设 f ( s ) f(s) f ( s ) A = S A=S A = S g ( S ) g(S) g ( S ) A ⊆ S A \subseteq S A ⊆ S
g ( S ) = ∑ S ⊆ T f ( T ) ⟺ f ( S ) = ∑ S ⊆ T ( − 1 ) ∣ T ∣ − ∣ S ∣ g ( T ) g(S) = \sum_{S \subseteq T} f(T) \iff f(S) = \sum_{S \subseteq T} (-1)^{|T|-|S|}g(T)
g ( S ) = S ⊆ T ∑ f ( T ) ⟺ f ( S ) = S ⊆ T ∑ ( − 1 ) ∣ T ∣ − ∣ S ∣ g ( T )
定义第一类斯特林数 [ n m ] \begin{bmatrix}n \\ m\end{bmatrix} [ n m ] n n n m m m ( 1 , 2 , 3 , 4 ) (1,2,3,4) ( 1 , 2 , 3 , 4 ) ( 2 , 3 , 4 , 1 ) (2,3,4,1) ( 2 , 3 , 4 , 1 ) ( 1 , 2 , 3 , 4 ) (1,2,3,4) ( 1 , 2 , 3 , 4 ) ( 4 , 3 , 2 , 1 ) (4,3,2,1) ( 4 , 3 , 2 , 1 )
[ n m ] = [ n − 1 m − 1 ] + ( n − 1 ) [ n − 1 m ] \begin{bmatrix}n\\m\end{bmatrix} = \begin{bmatrix} n-1 \\ m-1 \end{bmatrix} + (n-1) \begin{bmatrix} n-1 \\ m \end{bmatrix}
[ n m ] = [ n − 1 m − 1 ] + ( n − 1 ) [ n − 1 m ]
这个递推式就是考虑元素 n n n n − 1 n-1 n − 1
∑ i = 0 n [ n i ] = n ! \sum_{i=0}^n \begin{bmatrix} n \\ i \end{bmatrix} = n!
i = 0 ∑ n [ n i ] = n !
定义第二类斯特林数 { n m } \begin{Bmatrix} n \\ m\end{Bmatrix} { n m } n n n m m m
{ n m } = { n − 1 m − 1 } + m { n − 1 m } \begin{Bmatrix} n \\ m \end{Bmatrix} = \begin{Bmatrix} n-1 \\ m-1 \end{Bmatrix} + m\begin{Bmatrix} n-1 \\ m \end{Bmatrix}
{ n m } = { n − 1 m − 1 } + m { n − 1 m }
就是考虑元素 n n n
可以显然发现这个结论:
[ n m ] ≥ { n m } \begin{bmatrix} n \\ m\end{bmatrix} \ge \begin{Bmatrix} n \\ m \end{Bmatrix}
[ n m ] ≥ { n m }
因为一个圆排列只对应一个集合,而一个集合可以对应多个圆排列。
斯特林数最关键的应用就是:普通幂、上升幂、下降幂之间的转换。x n ‾ = x × ( x − 1 ) × ( x − 2 ) × ⋯ × ( x − n + 1 ) x^{\underline{n}} = x\times (x-1) \times (x-2) \times \cdots \times (x-n+1) x n = x × ( x − 1 ) × ( x − 2 ) × ⋯ × ( x − n + 1 ) x n ‾ = x × ( x + 1 ) × ( x + 2 ) × ⋯ × ( x + n − 1 ) x^{\overline{n}} = x \times (x+1) \times (x+2) \times \cdots \times (x+n-1) x n = x × ( x + 1 ) × ( x + 2 ) × ⋯ × ( x + n − 1 ) x < n x < n x < n x n ‾ = 0 x^{\underline{n}} = 0 x n = 0
普通幂转下降幂:
x n = ∑ i = 0 n { n i } x i ‾ x^n = \sum_{i=0}^n \begin{Bmatrix} n \\ i \end{Bmatrix} x^{\underline{i}}
x n = i = 0 ∑ n { n i } x i
证明:n = 0 n=0 n = 0 [ 0 , n − 1 ] [0,n-1] [ 0 , n − 1 ] n n n
∑ i = 0 n { n i } x i ‾ = ∑ i = 0 n { n − 1 i − 1 } x i ‾ + ∑ i = 0 n i × { n − 1 i } x i ‾ = ∑ i = 0 n − 1 { n − 1 i } x i + 1 ‾ + ∑ i = 0 n − 1 i × { n − 1 i } x i ‾ = ∑ i = 0 n − 1 ( x − i ) × { n − 1 i } x i ‾ + ∑ i = 0 n − 1 i × { n − 1 i } x i ‾ = x × ∑ i = 0 n { n i } x i ‾ = x × x n − 1 = x n \begin{aligned}
&\sum_{i=0}^{n} \begin{Bmatrix} n \\ i \end{Bmatrix} x^{\underline{i}} \\
&= \sum_{i=0}^{n} \begin{Bmatrix} n-1 \\ i-1 \end{Bmatrix}x^{\underline{i}} + \sum_{i=0}^n i \times \begin{Bmatrix} n-1 \\ i \end{Bmatrix} x^{\underline{i}} \\
&= \sum_{i=0}^{n-1} \begin{Bmatrix} n-1 \\ i \end{Bmatrix} x^{\underline{i+1}} + \sum_{i=0}^{n-1} i \times \begin{Bmatrix} n-1 \\ i \end{Bmatrix} x^{\underline{i}} \\
&= \sum_{i=0}^{n-1} (x-i) \times \begin{Bmatrix} n-1 \\ i \end{Bmatrix} x^{\underline{i}} + \sum_{i=0}^{n-1} i \times \begin{Bmatrix} n-1 \\ i \end{Bmatrix} x^{\underline{i}} \\
&= x \times \sum_{i=0}^n \begin{Bmatrix} n \\ i \end{Bmatrix} x^{\underline{i}} \\
&= x \times x^{n-1} \\
&= x^n
\end{aligned}
i = 0 ∑ n { n i } x i = i = 0 ∑ n { n − 1 i − 1 } x i + i = 0 ∑ n i × { n − 1 i } x i = i = 0 ∑ n − 1 { n − 1 i } x i + 1 + i = 0 ∑ n − 1 i × { n − 1 i } x i = i = 0 ∑ n − 1 ( x − i ) × { n − 1 i } x i + i = 0 ∑ n − 1 i × { n − 1 i } x i = x × i = 0 ∑ n { n i } x i = x × x n − 1 = x n
上升幂转通常幂:
x n ‾ = ∑ i = 0 n [ n i ] x i x^{\overline{n}} = \sum_{i=0}^n \begin{bmatrix} n \\ i \end{bmatrix} x^i
x n = i = 0 ∑ n [ n i ] x i
证明同上。
下降幂转通常幂:
x n ‾ = ∑ i = 0 n ( − 1 ) n − i { n i } x i x^{\underline{n}} = \sum_{i=0}^n (-1)^{n-i} \begin{Bmatrix} n \\ i \end{Bmatrix} x^i
x n = i = 0 ∑ n ( − 1 ) n − i { n i } x i
通常幂转上升幂:
x n = ∑ i = 0 n ( − 1 ) n − i [ n i ] x i ‾ x^{n} = \sum_{i=0}^n (-1)^{n-i} \begin{bmatrix} n \\ i \end{bmatrix} x^{\overline{i}}
x n = i = 0 ∑ n ( − 1 ) n − i [ n i ] x i
上述两个式子的证明:
x n ‾ = ( − 1 ) n × ( − x ) n ‾ x^{\underline{n}} = (-1)^n \times (-x)^{\overline{n}}
x n = ( − 1 ) n × ( − x ) n
将这个式子分别带入第一、二个公式即可得到这两个式子。
反转公式:
∑ i = m n { n i } [ i m ] ( − 1 ) n − i = [ m = n ] ∑ i = m n [ n i ] { i m } ( − 1 ) n − i = [ m = n ] \sum_{i=m}^n \begin{Bmatrix} n \\ i \end{Bmatrix} \begin{bmatrix} i \\ m \end{bmatrix} (-1)^{n-i} = [m = n] \\
\sum_{i=m}^n \begin{bmatrix} n \\ i \end{bmatrix} \begin{Bmatrix} i \\ m \end{Bmatrix} (-1)^{n-i}= [m = n] \\
i = m ∑ n { n i } [ i m ] ( − 1 ) n − i = [ m = n ] i = m ∑ n [ n i ] { i m } ( − 1 ) n − i = [ m = n ]
证明:
斯特林反演:
f ( n ) = ∑ i = 0 n [ n i ] g ( i ) ⟺ g ( n ) = ∑ i = 0 n ( − 1 ) n − i { n i } f ( i ) f ( n ) = ∑ i = 0 n { n i } g ( i ) ⟺ g ( n ) = ∑ i = 0 n ( − 1 ) n − i [ n i ] f ( i ) f ( n ) = ∑ i = n [ i n ] g ( i ) ⟺ g ( n ) = ∑ i = n ( − 1 ) i − n { i n } f ( i ) f ( n ) = ∑ i = n { i n } g ( i ) ⟺ g ( n ) = ∑ i = n ( − 1 ) i − n [ i n ] f ( i ) f(n) = \sum_{i=0}^n \begin{bmatrix} n \\ i \end{bmatrix} g(i) \iff g(n) = \sum_{i=0}^n (-1)^{n-i} \begin{Bmatrix} n \\ i \end{Bmatrix} f(i) \\
f(n) = \sum_{i=0}^n \begin{Bmatrix} n \\ i \end{Bmatrix} g(i) \iff g(n) = \sum_{i=0}^n (-1)^{n-i} \begin{bmatrix} n \\ i \end{bmatrix} f(i) \\
f(n) = \sum_{i=n} \begin{bmatrix} i \\ n \end{bmatrix} g(i) \iff g(n) = \sum_{i=n} (-1)^{i-n} \begin{Bmatrix} i \\ n \end{Bmatrix} f(i) \\
f(n) = \sum_{i=n} \begin{Bmatrix} i \\ n \end{Bmatrix} g(i) \iff g(n) = \sum_{i=n} (-1)^{i-n} \begin{bmatrix} i \\ n \end{bmatrix} f(i) \\
f ( n ) = i = 0 ∑ n [ n i ] g ( i ) ⟺ g ( n ) = i = 0 ∑ n ( − 1 ) n − i { n i } f ( i ) f ( n ) = i = 0 ∑ n { n i } g ( i ) ⟺ g ( n ) = i = 0 ∑ n ( − 1 ) n − i [ n i ] f ( i ) f ( n ) = i = n ∑ [ i n ] g ( i ) ⟺ g ( n ) = i = n ∑ ( − 1 ) i − n { i n } f ( i ) f ( n ) = i = n ∑ { i n } g ( i ) ⟺ g ( n ) = i = n ∑ ( − 1 ) i − n [ i n ] f ( i )
下面只证明一下第一个式子的充分性,其余的都可以类比地推出。
g ( n ) = ∑ i = 0 n [ i = n ] g ( i ) = ∑ i = 0 n ( ∑ j = i n { n j } [ j i ] ( − 1 ) n − j g ( i ) ) = ∑ j = 0 n ( − 1 ) n − j { n j } ( ∑ i = 0 j [ j i ] g ( i ) ) = ∑ j = 0 n ( − 1 ) n − j { n j } f ( j ) \begin{aligned}
g(n)
&= \sum_{i=0}^n [i=n] g(i) \\
&= \sum_{i=0}^n \left(\sum_{j=i}^n \begin{Bmatrix} n \\ j \end{Bmatrix} \begin{bmatrix} j \\ i \end{bmatrix} (-1)^{n-j} g(i)\right) \\
&= \sum_{j=0}^n (-1)^{n-j} \begin{Bmatrix} n \\ j \end{Bmatrix} \left(\sum_{i=0}^j \begin{bmatrix} j \\ i \end{bmatrix} g(i)\right) \\
&= \sum_{j=0}^n (-1)^{n-j} \begin{Bmatrix} n \\ j \end{Bmatrix}f(j)
\end{aligned}
g ( n ) = i = 0 ∑ n [ i = n ] g ( i ) = i = 0 ∑ n ( j = i ∑ n { n j } [ j i ] ( − 1 ) n − j g ( i ) ) = j = 0 ∑ n ( − 1 ) n − j { n j } ( i = 0 ∑ j [ j i ] g ( i ) ) = j = 0 ∑ n ( − 1 ) n − j { n j } f ( j )
若给定矩阵 A , B A,B A , B C = A × B C = A \times B C = A × B c i , j = ∑ k ( A i , k × B k , j ) c_{i,j} = \sum_{k} (A_{i,k} \times B_{k,j}) c i , j = ∑ k ( A i , k × B k , j ) A , B A,B A , B A A A B B B C C C ( i , j ) (i,j) ( i , j ) A A A i i i B B B j j j C C C A A A B B B
矩阵乘法满足结合律,但不满足交换律,即若我们要计算 A k A^k A k
我们可以将矩阵乘法中的运算更换,比如换成:c i , j = max k ( A i , k + B k , j ) c_{i,j} = \max_{k} (A_{i,k} + B_{k,j}) c i , j = max k ( A i , k + B k , j ) max + \max+ max + d p dp d p O ( log n ) O(\log n) O ( log n ) d p dp d p d p dp d p
请查看:
【学习笔记】高斯消元
本文只会扩展一下高斯消元的应用,主要是这种加减消元法的思想。
记 ⊕ \oplus ⊕ xor 操作,解下列方程组:
a 1 , 1 x 1 ⊕ a 1 , 2 x 2 ⊕ ⋯ a 1 , n x n = y 1 a 2 , 1 x 1 ⊕ a 2 , 2 x 2 ⊕ ⋯ a 2 , n x n = y 2 ⋯ a m , 1 x 1 ⊕ a m , 2 x 2 ⊕ ⋯ a m , n x n = y m a_{1,1} x_1 \oplus a_{1,2} x_2 \oplus \cdots a_{1,n} x_n = y_1 \\
a_{2,1} x_1 \oplus a_{2,2} x_2 \oplus \cdots a_{2,n} x_n = y_2 \\
\cdots\\
a_{m,1} x_1 \oplus a_{m,2} x_2 \oplus \cdots a_{m,n} x_n = y_m\\
a 1 , 1 x 1 ⊕ a 1 , 2 x 2 ⊕ ⋯ a 1 , n x n = y 1 a 2 , 1 x 1 ⊕ a 2 , 2 x 2 ⊕ ⋯ a 2 , n x n = y 2 ⋯ a m , 1 x 1 ⊕ a m , 2 x 2 ⊕ ⋯ a m , n x n = y m
其中 a i , j ∈ { 0 , 1 } a_{i,j} \in \{0,1\} a i , j ∈ { 0 , 1 }
注意到一点 a ⊕ a = 0 a \oplus a = 0 a ⊕ a = 0 bitset 优化到 O ( n 3 w ) O(\frac{n^3}{w}) O ( w n 3 )
对于方阵 A A A A − 1 A^{-1} A − 1 A × A − 1 = A − 1 × A = I A \times A^{-1} = A^{-1} \times A = I A × A − 1 = A − 1 × A = I A A A A − 1 A^{-1} A − 1 I n I_n I n n × n n\times n n × n
构造一个 n × 2 n n \times 2n n × 2 n ( A , I n ) (A,I_n) ( A , I n )
通过高斯消元将矩阵变成 ( I n , A − 1 ) (I_n,A^{-1}) ( I n , A − 1 ) A A A A − 1 A^{-1} A − 1 I n I_n I n A A A
对于一个 n × n n \times n n × n A A A
det ( A ) = ∑ σ ∈ S n sgn ( σ ) ∏ i = 1 n a i , σ i \det(A) = \sum_{\sigma \in S_n} \text{sgn}(\sigma)\prod_{i=1}^n a_{i,\sigma_i}
det ( A ) = σ ∈ S n ∑ sgn ( σ ) i = 1 ∏ n a i , σ i
其中 S n S_n S n n n n sgn ( σ ) \text{sgn}(\sigma) sgn ( σ ) σ \sigma σ σ \sigma σ sgn ( σ ) = 1 \text{sgn}(\sigma) = 1 sgn ( σ ) = 1 sgn ( σ ) = − 1 \text{sgn}(\sigma) = -1 sgn ( σ ) = − 1
行列式有如下性质:
交换两行(列)行列式的值取反x , y x,y x , y ∏ i = 1 n a i , σ i \prod_{i=1}^n a_{i,\sigma_i} ∏ i = 1 n a i , σ i σ x \sigma_x σ x σ y \sigma_y σ y σ x , σ y \sigma_x,\sigma_y σ x , σ y p ∈ ( x , y ) p\in(x,y) p ∈ ( x , y ) σ p \sigma_p σ p σ x , σ y \sigma_x,\sigma_y σ x , σ y p ∈ [ 1 , x ) ⋃ ( y , n ] p\in [1,x) \bigcup (y,n] p ∈ [ 1 , x ) ⋃ ( y , n ] σ p \sigma_p σ p σ x , σ y \sigma_x,\sigma_y σ x , σ y 1 1 1 − 1 -1 − 1
将一行(列)加到另一行(列)上行列式的值不变x x x y y y σ \sigma σ σ x \sigma_x σ x σ y \sigma_y σ y σ ′ \sigma' σ ′ sgn ( σ ) = − sgn ( σ ′ ) \text{sgn}(\sigma) = -\text{sgn}(\sigma') sgn ( σ ) = − sgn ( σ ′ )
若行列式只有 a i , j ( i ≤ j ) a_{i,j}(i \le j) a i , j ( i ≤ j ) ∏ i = 1 n a i , i \prod_{i=1}^n a_{i,i} ∏ i = 1 n a i , i σ \sigma σ ∏ i = 1 n a i , σ i \prod_{i=1}^n a_{i,\sigma_i} ∏ i = 1 n a i , σ i 0 0 0 σ = { 1 , 2 , 3 , 4 , ⋯ , n } \sigma = \{1,2,3,4,\cdots,n\} σ = { 1 , 2 , 3 , 4 , ⋯ , n } sgn ( σ ) = 1 \text{sgn}(\sigma) = 1 sgn ( σ ) = 1 ∏ i = 1 n a i , i \prod_{i=1}^n a_{i,i} ∏ i = 1 n a i , i
将行列式某行(列)同时乘 k k k k k k σ \sigma σ a i , σ i a_{i,\sigma_i} a i , σ i k k k k k k
通过上述性质我们就可以直接通过高斯消元将行列式消成上三角,然后对角线元素的乘积就是行列式的值。− 1 -1 − 1
LGV 引理常用于解决 DAG 上不相交路径(权值)计数问题
记 w ( P ) w(P) w ( P ) P P P 1 1 1 e ( u , v ) e(u,v) e ( u , v ) u u u v v v P P P w ( P ) w(P) w ( P ) A A A B B B n n n
M = [ e ( A 1 , B 1 ) e ( A 1 , B 2 ) ⋯ e ( A 1 , B n ) e ( A 2 , B 1 ) e ( A 2 , B 2 ) ⋯ e ( A 2 , B n ) ⋯ ⋯ ⋯ ⋯ e ( A n , B 1 ) e ( A n , B 2 ) ⋯ e ( A n , B n ) ] M =
\begin{bmatrix}
e(A_1,B_1) &e(A_1,B_2) &\cdots &e(A_1,B_n) \\
e(A_2,B_1) &e(A_2,B_2) &\cdots &e(A_2,B_n) \\
\cdots &\cdots &\cdots &\cdots \\
e(A_n,B_1) &e(A_n,B_2) &\cdots &e(A_n,B_n) \\
\end{bmatrix}
M = ⎣ ⎢ ⎢ ⎢ ⎡ e ( A 1 , B 1 ) e ( A 2 , B 1 ) ⋯ e ( A n , B 1 ) e ( A 1 , B 2 ) e ( A 2 , B 2 ) ⋯ e ( A n , B 2 ) ⋯ ⋯ ⋯ ⋯ e ( A 1 , B n ) e ( A 2 , B n ) ⋯ e ( A n , B n ) ⎦ ⎥ ⎥ ⎥ ⎤
感觉这个如果不给例题就实在是太抽象了。
例题 CF348D Turtles :n n n m m m ( 1 , 1 ) (1,1) ( 1 , 1 ) ( n , m ) (n,m) ( n , m ) ( 1 , 1 ) (1,1) ( 1 , 1 ) ( n , m ) (n,m) ( n , m ) ( n , m ) (n,m) ( n , m ) 1 0 9 + 7 10^9+7 1 0 9 + 7
考虑我们从 ( 1 , 1 ) (1,1) ( 1 , 1 ) ( 1 , 2 ) (1,2) ( 1 , 2 ) ( 2 , 1 ) (2,1) ( 2 , 1 ) ( n , m ) (n,m) ( n , m ) ( n − 1 , m ) (n-1,m) ( n − 1 , m ) ( n , m − 1 ) (n,m-1) ( n , m − 1 ) A = { ( 1 , 2 ) , ( 2 , 1 ) } A = \{(1,2),(2,1)\} A = { ( 1 , 2 ) , ( 2 , 1 ) } B = { ( n − 1 , m ) , ( n , m − 1 ) } B = \{(n-1,m),(n,m-1)\} B = { ( n − 1 , m ) , ( n , m − 1 ) } e ( i , j ) e(i,j) e ( i , j ) i i i j j j O ( n m ) O(nm) O ( n m ) d p dp d p
矩阵树定理可以解决给定一张图,求其生成树个数,这里要求给定的图没有自环。G = ( V , E ) G = (V,E) G = ( V , E ) m i , j m_{i,j} m i , j ( i , j ) (i,j) ( i , j ) d e g i deg_i d e g i i i i L L L
L i , j = { − m i , j i ≠ j d e g i i = j L_{i,j} =
\begin{cases}
-m_{i,j} & i\not= j \\
deg_i & i = j
\end{cases}
L i , j = { − m i , j d e g i i = j i = j
则生成树个数为 L L L
下面考虑有向图的情况。m i , j m_{i,j} m i , j i i i j j j
L i , j o u t = { − m i , j i ≠ j d e g i o u t i = j L_{i,j}^{out} =
\begin{cases}
-m_{i,j} & i\not= j\\
deg_i^{out} & i = j
\end{cases}
L i , j o u t = { − m i , j d e g i o u t i = j i = j
定义入度拉普拉斯矩阵为:
L i , j i n = { − m i , j i ≠ j d e g i i n i = j L_{i,j}^{in} =
\begin{cases}
-m_{i,j} & i\not= j \\
deg_i^{in} & i = j
\end{cases}
L i , j i n = { − m i , j d e g i i n i = j i = j
记图 G G G r r r t r o o t ( G , r ) t^{root}(G,r) t r o o t ( G , r ) G G G r r r t l e a f ( G , r ) t^{leaf}(G,r) t l e a f ( G , r )
t r o o t ( G , k ) = det L o u t ( 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n ) t l e a f ( G , k ) = det L i n ( 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n ) t^{root}(G,k) = \det L^{out}\binom{1,2,3,\cdots,k-1,k+1,\cdots,n}{1,2,3,\cdots,k-1,k+1,\cdots,n} \\
t^{leaf}(G,k) = \det L^{in} \binom{1,2,3,\cdots,k-1,k+1,\cdots,n}{1,2,3,\cdots,k-1,k+1,\cdots,n}
t r o o t ( G , k ) = det L o u t ( 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n ) t l e a f ( G , k ) = det L i n ( 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n )
其中定义 L ( 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ n ) L\binom{1,2,3,\cdots,k-1,k+1,\cdots,n}{1,2,3,\cdots,k-1,k+1,\cdots n} L ( 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ n 1 , 2 , 3 , ⋯ , k − 1 , k + 1 , ⋯ , n ) L L L k k k k k k
定义 t r o o t ( G , k ) t^{root}(G,k) t r o o t ( G , k ) G G G k k k G G G G G G
t r o o t ( G , k ) ∏ v ∈ V ( d e g v − 1 ) ! t^{root}(G,k)\prod_{v \in V} (deg_v - 1)!
t r o o t ( G , k ) v ∈ V ∏ ( d e g v − 1 ) !
d e g v deg_v d e g v k k k u , v u,v u , v t r o o t ( G , x ) = t r o o t ( G , y ) t^{root}(G,x) = t^{root}(G,y) t r o o t ( G , x ) = t r o o t ( G , y )
一种感性理解这个定理的方法:∏ v ∈ V ( d e g v − 1 ) ! \prod_{v \in V} (deg_v-1)! ∏ v ∈ V ( d e g v − 1 ) !
请查看:
【学习笔记】数论之生成函数基础 【学习笔记】拉格朗日插值
请查看:
【学习笔记】Burnside 定理和 Polya 定理
请查看:
【学习笔记】计算几何
请查看:
【学习笔记】博弈论 ---- 非偏博弈