ABC275Ex Monster

【题解】ABC275Ex Monster

题目描述：

给定 $n$ 以及两个长度为 $n$ 的正整数序列 $A_i,B_i$，你可以执行下述操作任意次：

• 选定任意整数 $l,r$，满足 $1 \le l \le r \le n$。
• 花费 $max_{i=l}^{r} \{B_i\}$ 的代价，将 $A_l,A_{l+1}, \dots A_r$ 中每个都减去 $1$。

请求出使得 $A_i$ 中元素全部 $\le 0$ 所需的最小代价。

$1 \le n \le 10^5, 1 \le A_i,B_i \le 10^9$。

题目分析：

考虑操作 $[l,r]$ 的代价是这段区间 $B$ 的最大值，也就是说设最大值为 $B_x$，那么我们选择的区间一定是以 $B_x$ 为最大值的极长的一段区间，对应笛卡尔树中 $x$ 的子树，所以我们的一次操作就相当于花费 $B_x$ 的代价，将 $x$ 子树中所有点的 $A$ 值减 $1$。
一个显然的 $dp$ 就是设 $dp[i][j]$ 表示以 $i$ 为根的子树中，对于所有 $i$ 子树内的点 $x$ 都有 $A_x \le j$ 的最小代价。
转移是简单的：

$$\begin{aligned} dp[i][j] &= \min_{k=\max(j,A_i)} \{dp[ls[i]][k] + dp[rs[i]][k] + (k-j) B_i\} \\ &= -B_i\times j + \min_{k=\max(j,A_i)} \{dp[ls[i]][k] + dp[rs[i]][k] + k \times B_i\} \end{aligned}$$

其中 $k$ 的边界是由以下限制得来的：

$$k \ge j \\ A_i - (k - j) \ge j$$

其实看到这个 $dp$ 状态就很有一种凸函数的感觉，所以打表之后会发现若将 $dp[i][j]$ 视为一个关于 $j$ 的函数，那么其是一个分段一次凸函数，即满足下图所示：

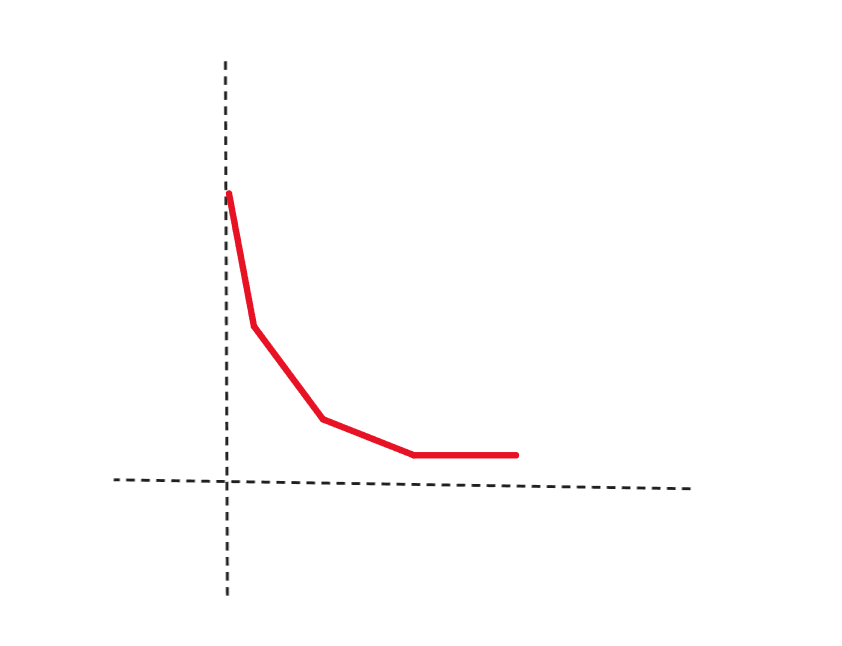
证明就是考虑几个分段一次凸函数相加依旧是一个分段一次凸函数即可。
考虑我们的转移对这个分段一次凸函数有什么影响，假设我们现在直接合并了 $dp[ls[i]]$ 和 $dp[rs[i]]$。
就是将在 $A[i]$ 之前的位置的图像抹平，在 $A[i]$ 之后的位置的图像加入一条斜率为 $B[i]$ 的一次函数。
然后再将所有位置加入一条斜率为 $-B[i]$ 的一次函数。
所以可以发现其实我们每一次至多增加 $O(1)$ 段，也就是说我们的段数为 $O(n)$。
上述过程如下图所示：

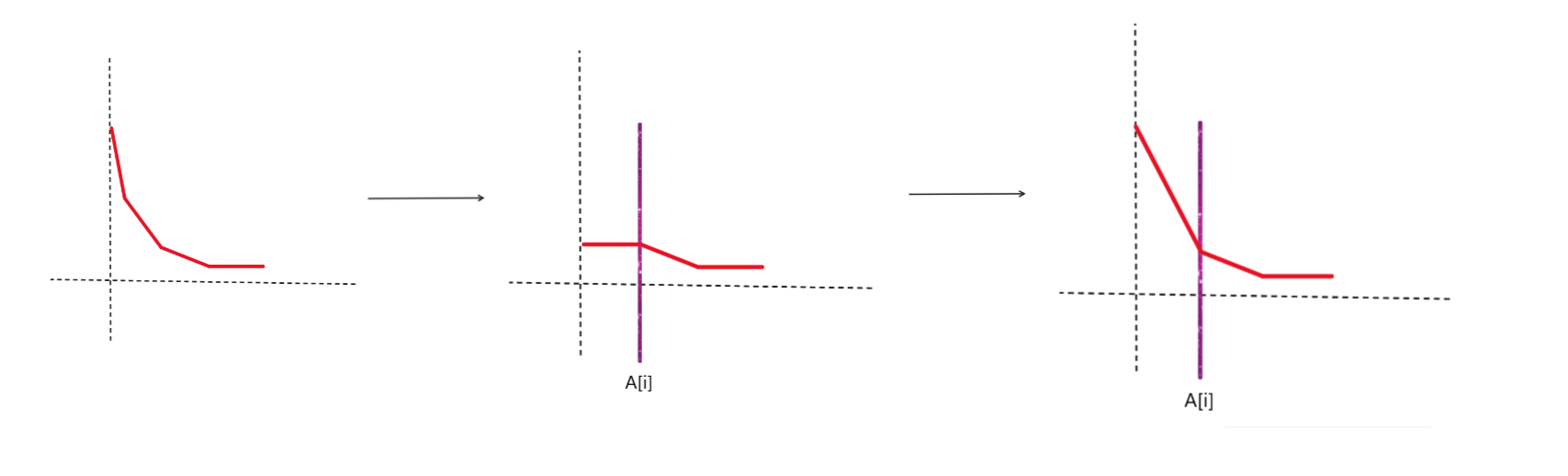
一个做法就是考虑使用可并堆维护每一个图像上的拐点和经过这个拐点之后一次函数斜率的变化量，堆内按拐点的 $x$ 坐标从小到大排序。
维护变化量的主要原因是因为我们要支持加入斜率为 $B[i]$ 和 $-B[i]$ 的直线，如果暴力遍历所有的段然后加显然就炸了，不如直接维护变化量这样在某一个位置单点加入即可，以及这个时候我们合并两个 $dp$ 值就直接堆的合并就可以实现斜率的相加。

代码实现的细节就是：
我们只需要维护出 $dp[0]$ 处的值，其它的维护好斜率即可。
对于将某一段抹平这个操作，因为我们只有 $O(n)$ 段所以可以暴力一段段地抹平，主要是这样可以直接维护出 $dp[0]$ 的变化。
而对于增加斜率为 $-B[i]$ 的直线对 $dp[0]$ 的影响，可以考虑将增加斜率为 $B[i]$ 的直线的操作放到序列的开头，这样直接扫过去就可以维护好对 $dp[0]$ 的影响，也可以同时维护好对后面部分斜率的影响。